

개요
우리가 집합이라는 개념을 생각했을 때 보통 아래의 그림처럼 벤-다이어그램으로 생각을 하곤 한다.▼
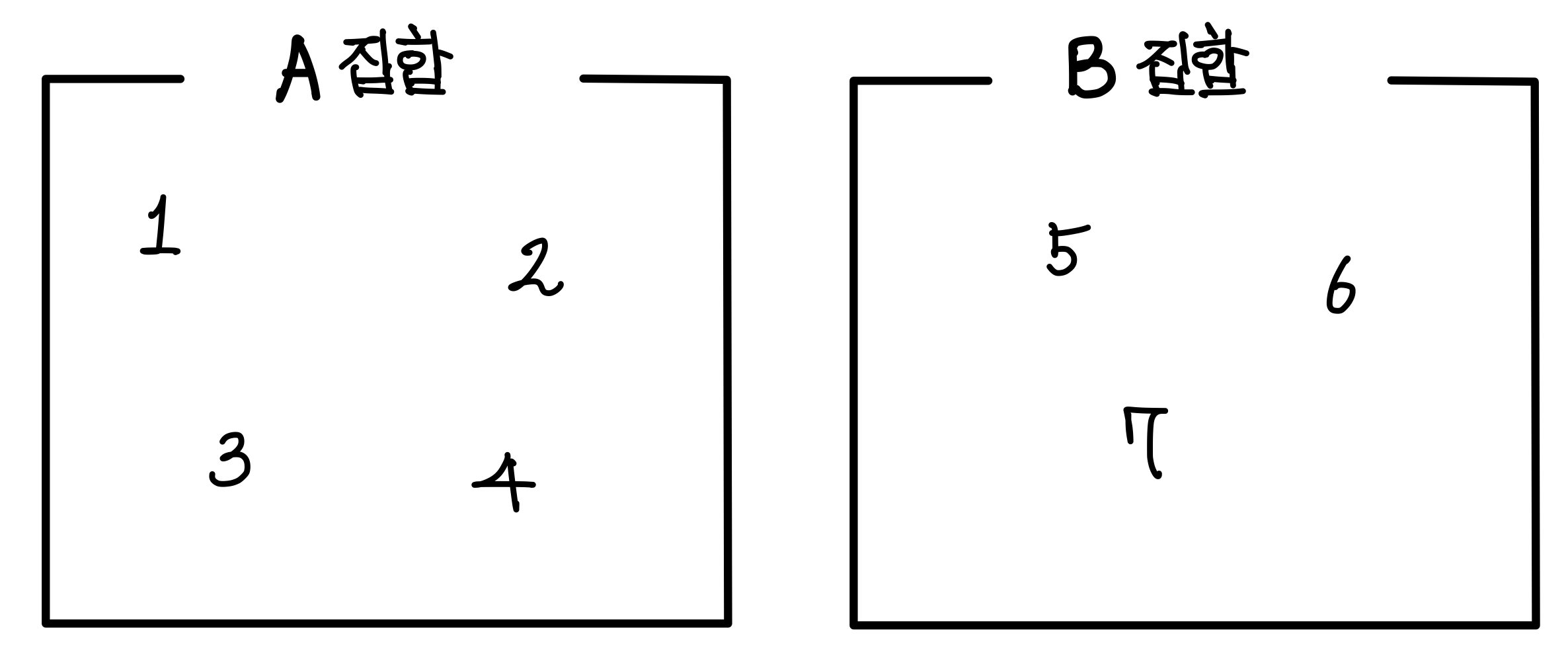
그런데 이런 집합이라면 아래와 같이 배열로 표현할 수 있다.▼
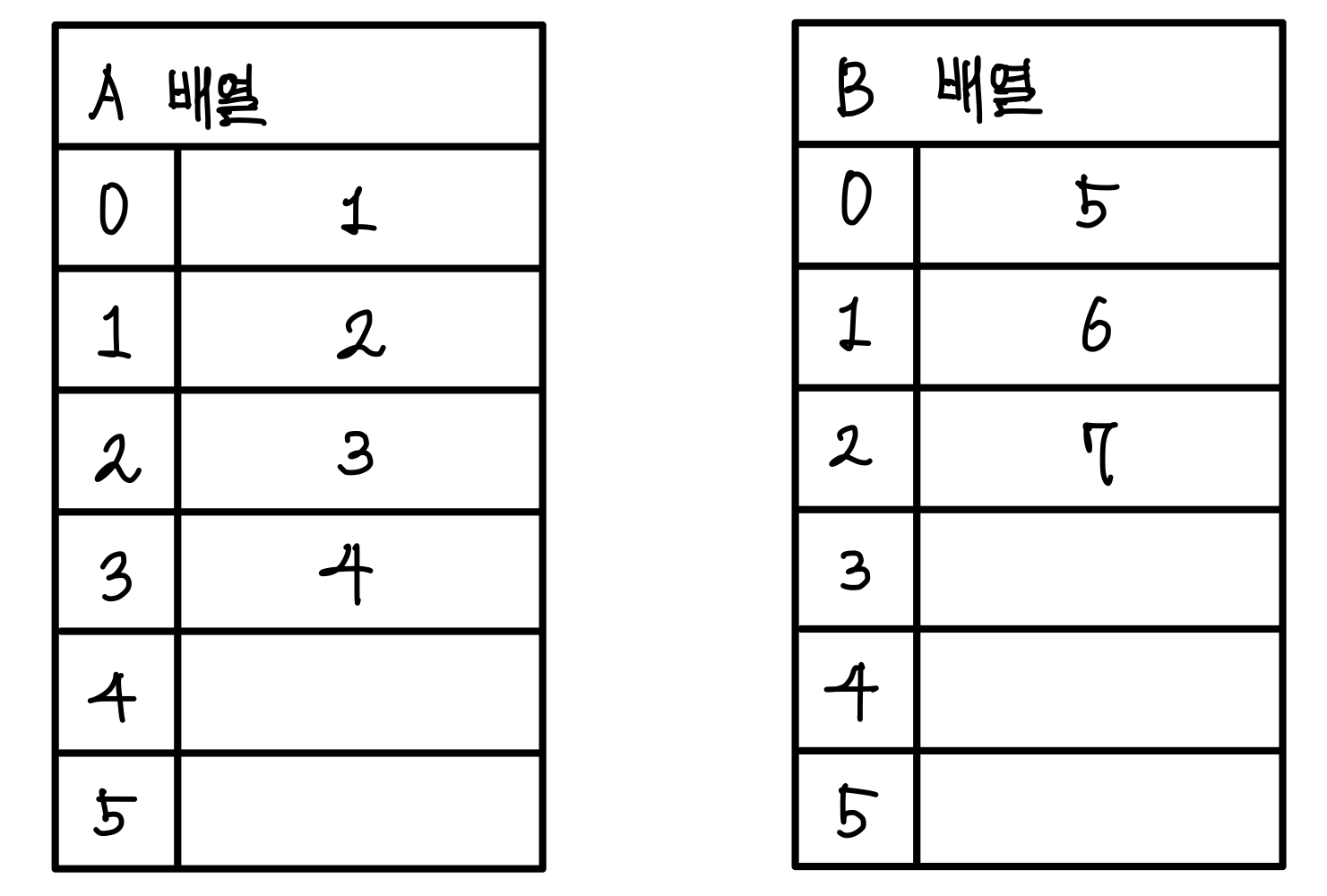
하지만 두 원소가 같은 집합에 있는지를 판단하라고 하면 약간 곤란해진다.
A집합에 있는 1 원소와 B집합에 있는 5 원소가 같은 집합에 있는지를 판단하려면 A집합이나 B집합을 다 확인해야한다.
A집합에 5 원소가 있는 지 없는 지, B집합에 1 원소가 있는지 없는 지를 확인해야한다. ▼
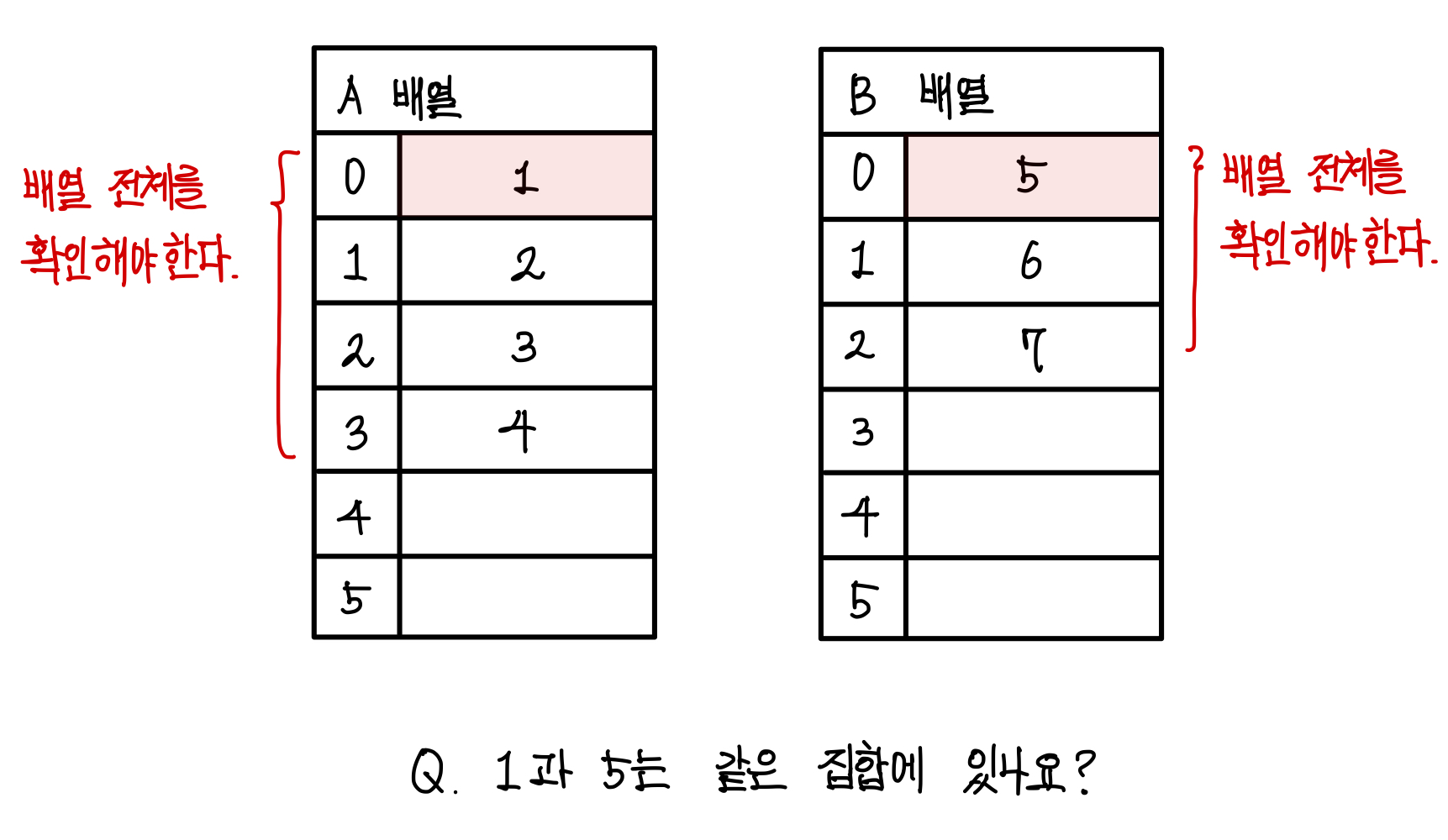
배열로 구현하게 되면 집합의 대표를 알아내기가 힘들어서 같은 원소에 대해서 또 확인하게 되면 같은 연산을 계속 수행해야한다.
심지어는 두 집합이 서로소인것을 알아내어 합한다고 했을 때도, 원소를 옮기는 과정에서의 연산도 적지않게 수행된다. ▼
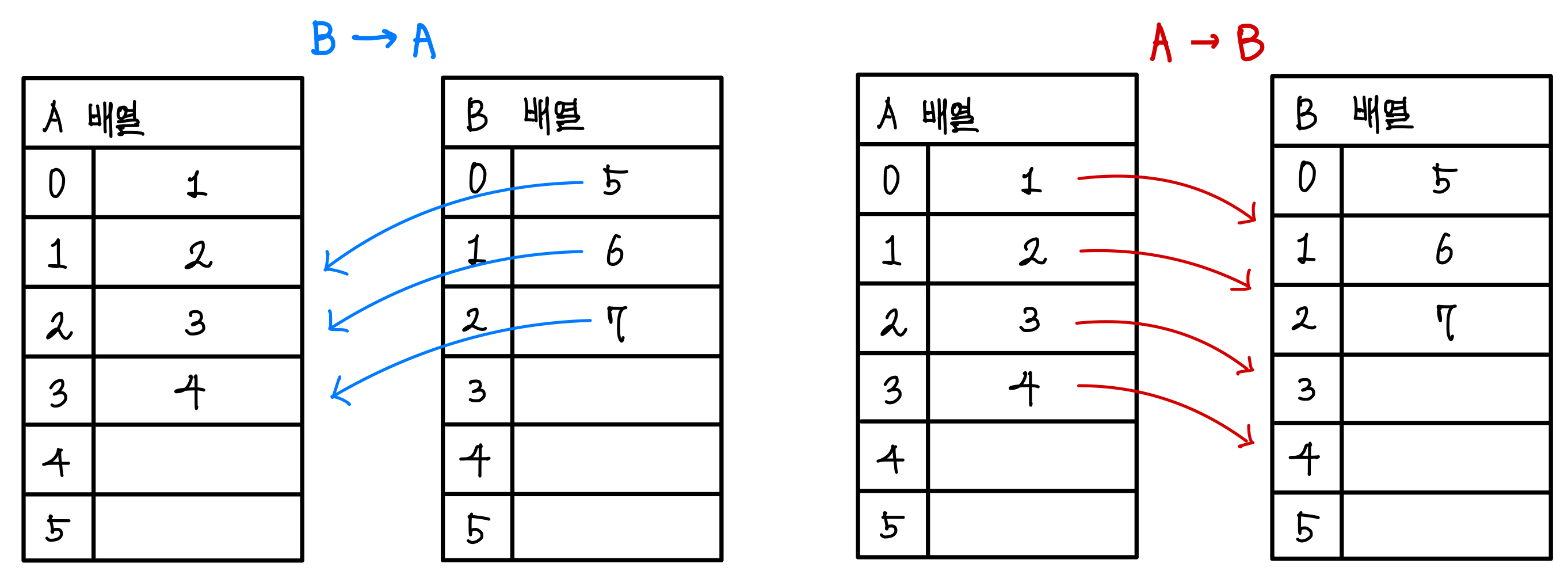
이런 집합에 대해서 표현을 할 때 배열을 이용하면 연산량이 많아지게 된다.
그렇다면 어떻게 이를 좀 더 효율적으로 수행할 수 있을까?
이는 Disjoint Set 자료구조를 통해 해결할 수 있다.
Disjoint Set
위의 문제를 해결하기 위해 Disjoint Set이라는 자료구조를 사용할 것이다.
Disjoint Set은 상호 배타적 집합 또는 서로소 집합이다.
서로소 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조이다.
Disjoint Set 자료구조를 사용하면 서로 다른 원소가 같은 집합에 속해있는지, 혹은 속해있지 않은지를 쉽게 판별할 수 있다.
허나 위의 예시와는 다른 점이 있다면 Disjoint Set 자료구조는 배열이 아닌 트리를 이용해서 표현한다는 것이다.▼
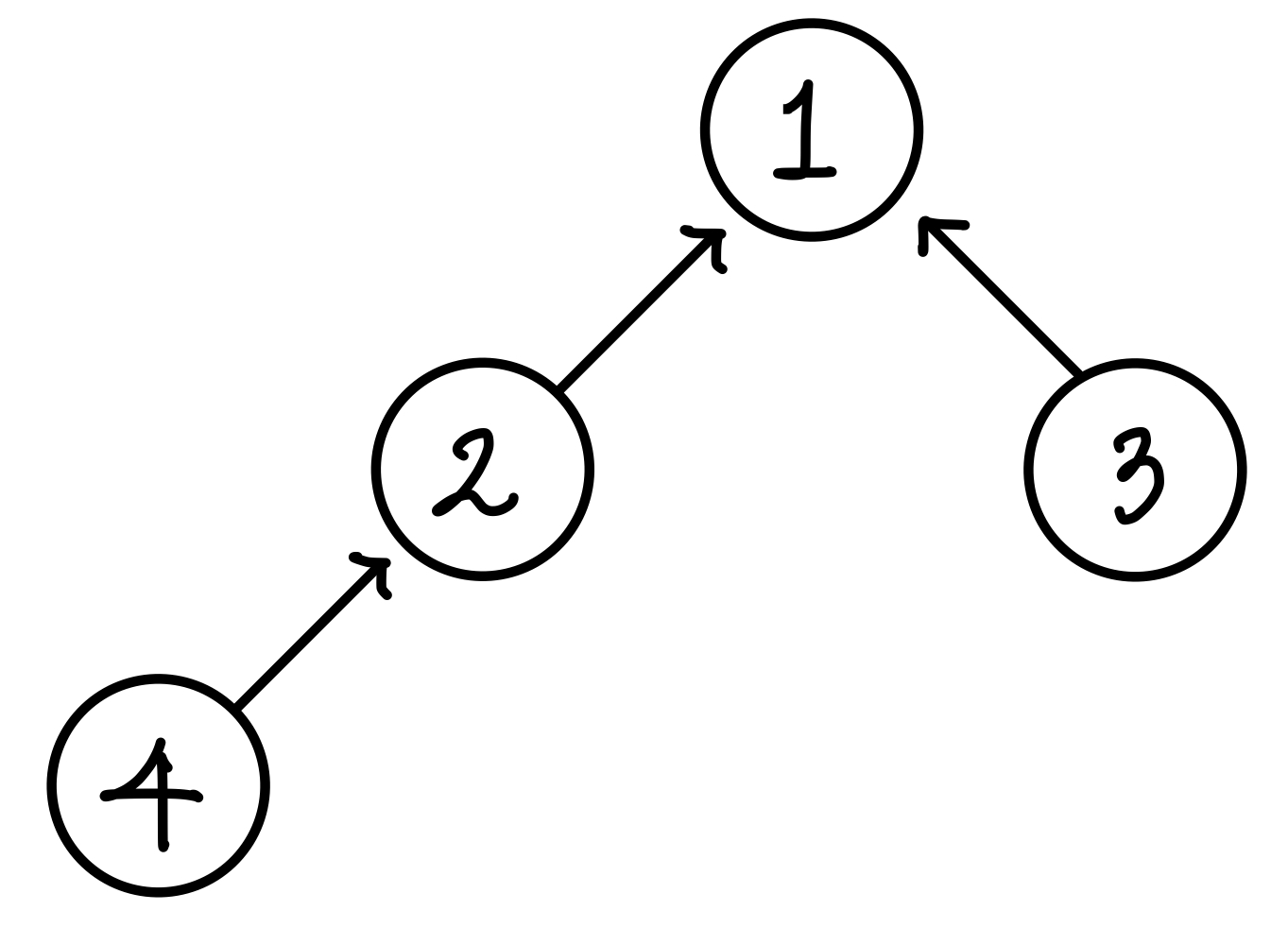
기본적으로 서로소인지 아닌지를 판별하는 방법은 루트를 비교하는 것이다.
원소는 중복되지 않는다고 가정하고, 각 원소의 루트가 무엇인지 적어준다.
아래와 같이 두 집합이 있다고 해보자.▼
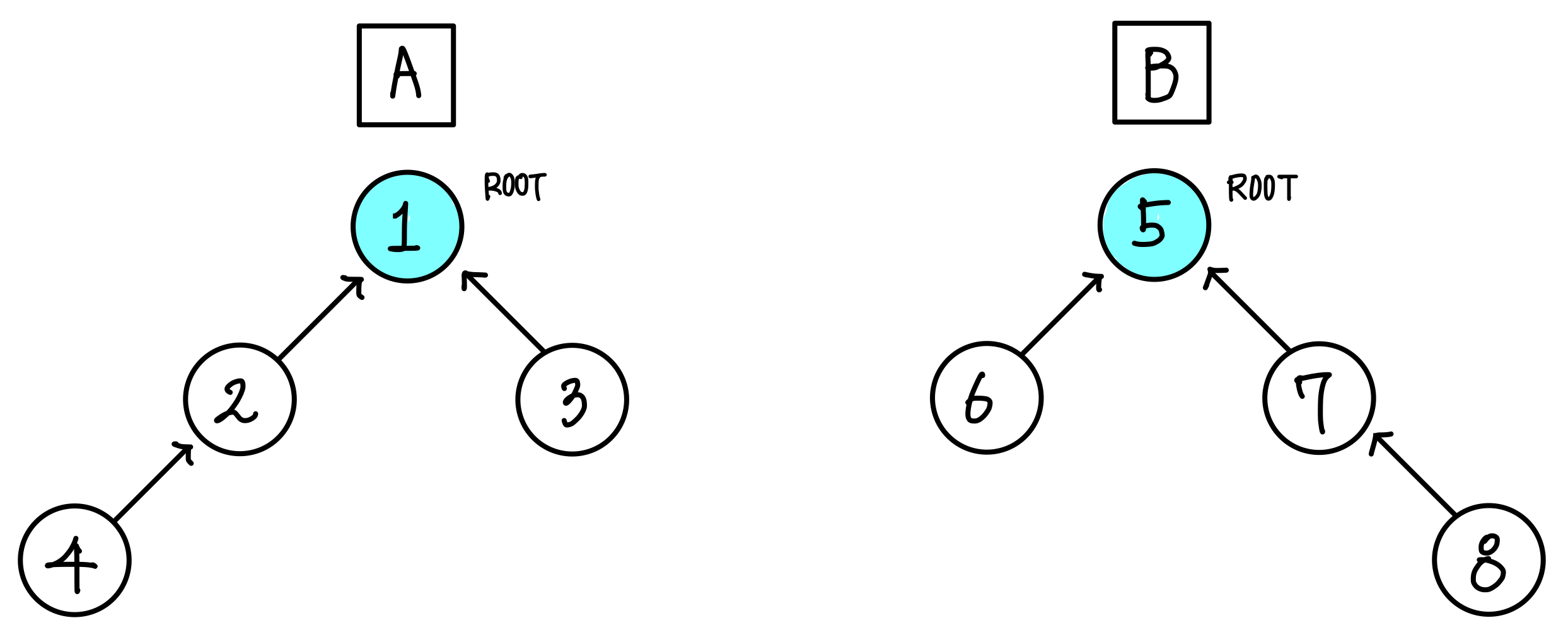
두 집합의 루트는 각각 1과 5로 다른 집합이다.
루트가 다르다는 것은 두 원소가 같은 집합에 있지 않다는 것을 뜻한다.
그래서 기존의 노드를 연결하는 연결리스트 방식이 아닌 배열 방식으로 트리를 표현할 것이다.
위의 그림을 배열처럼 표시하면 아래처럼 된다.▼
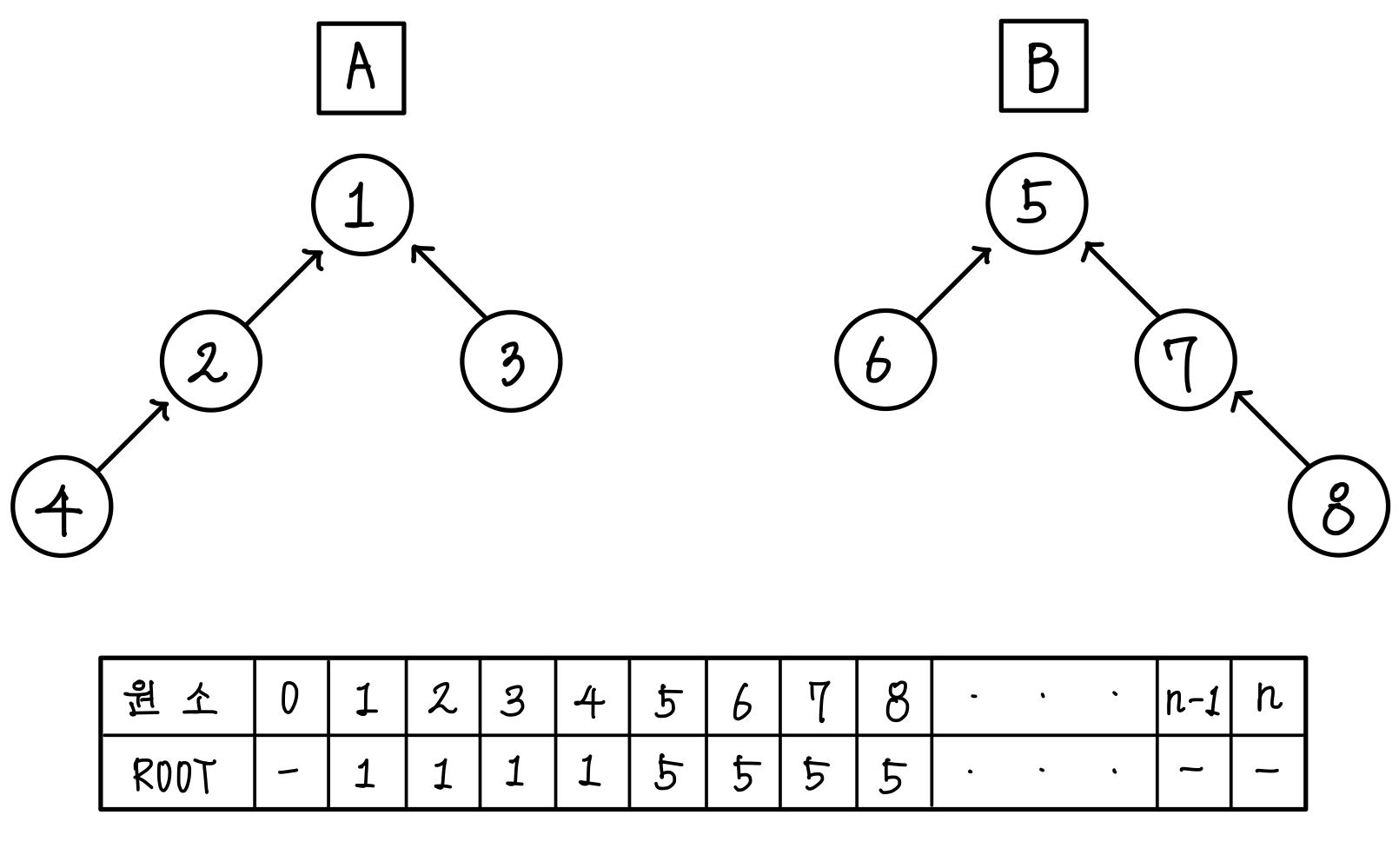
Union-Find 연산
보통 서로소 집합 자료 구조는 Union과 Find의 두 연산을 제공한다.
Find
Find 연산은 루트를 찾는 연산이다.
재귀함수를 통해 거듭해서 루트 노드를 찾아 올라간다.
루트 노드가 어떤 집합인지를 알려주는 것이기 때문에 부모 노드를 거슬러 올라가 루트 노드를 보면 된다.
예시를 한 번 보자.
아래와 같이 집합이 구성되어있고, 집합의 표현을 배열로 했다고 해보자.▼
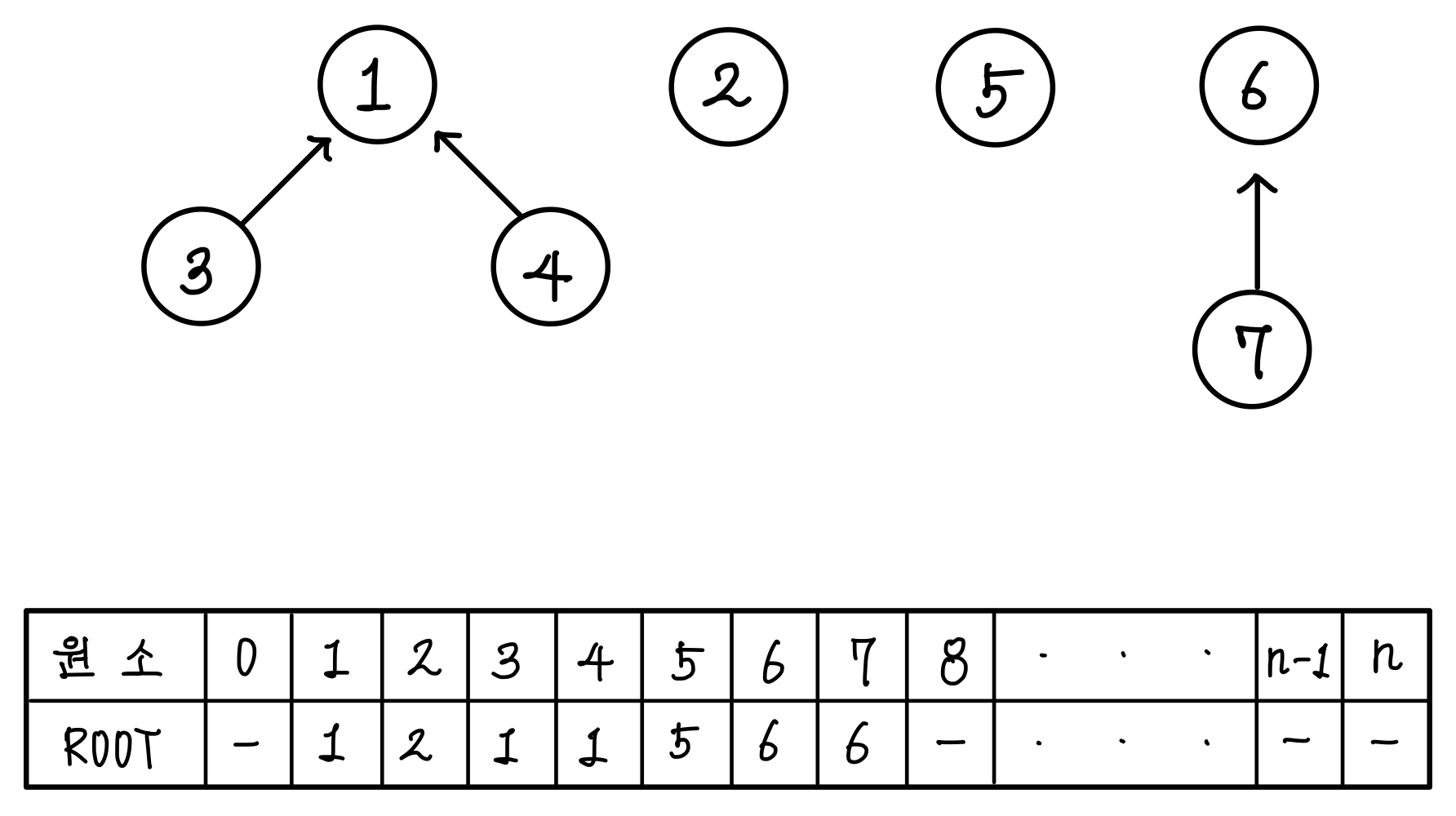
여기서 원소 3과 원소 7이 같은 집합에 속해 있는지 확인해본다고 해보자.
그러면 원소 3과 원소 7의 루트 값을 확인해보고 해당 루트 값의 원소의 루트 값을 확인해본다.
원소와 루트의 값이 같다면 최종 목적지에 도달한 것이므로 재귀를 멈춘다.▼
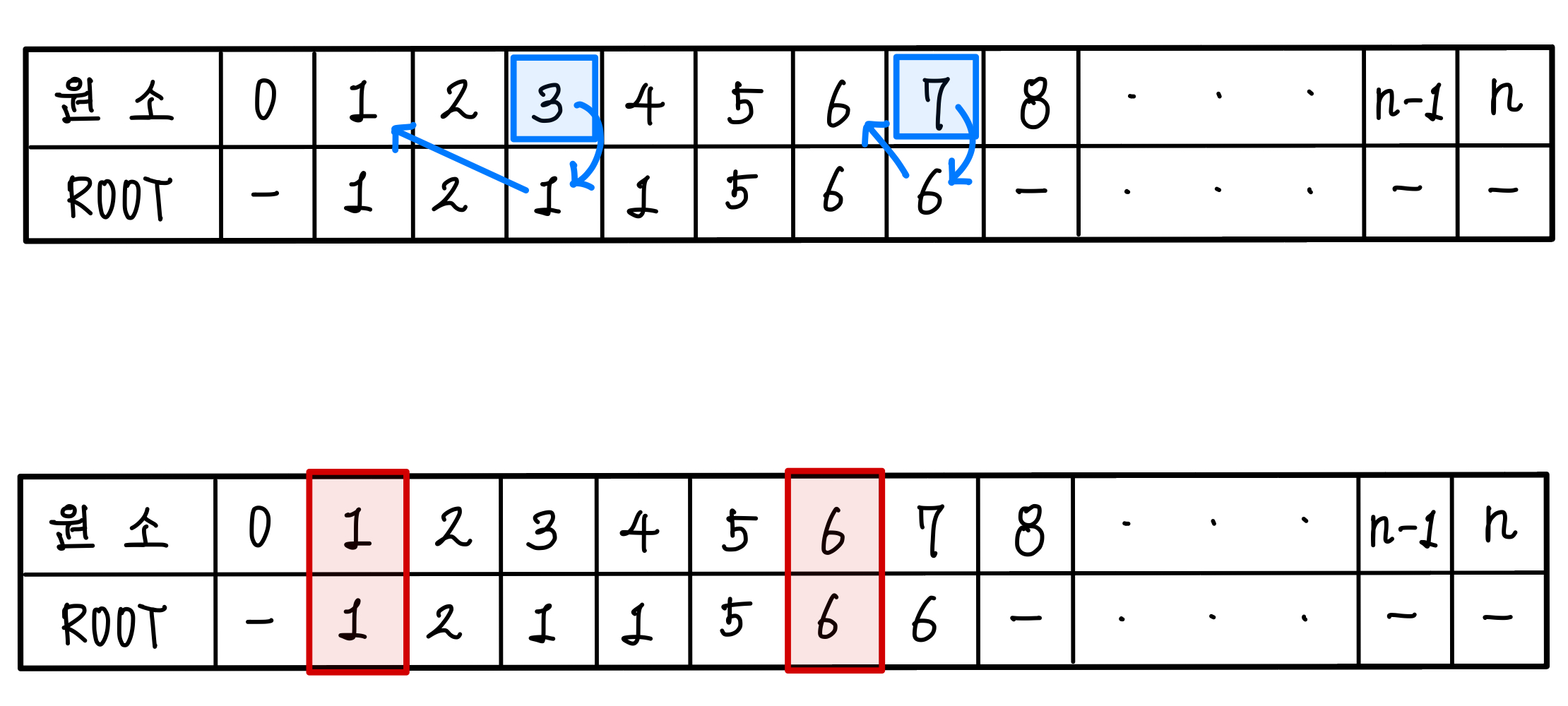
즉, 3의 루트는 1이고 7의 루트는 6이 된다.
둘의 루트가 다르므로 3과 7은 다른 집합에 있다고 판단한다. ▼

코드
int find_parent(int a) {
if (a == parent[a])
return a;
else
return find_parent(parent[a]);
}
Union
기존의 배열 방식으로 합집합 연산을 하게 되면 배열 요소를 옮기는데 꽤 많은 시간을 소모하게 된다.
하지만 트리로 구성하면 한 쪽의 루트 노드를 다른 쪽 루트 노드에 연결하는 것으로 합 연산을 할 수 있게 된다.
아래의 예시를 보면서 확인해보자.
A와 B의 두 집합이 있다고 해보자.▼
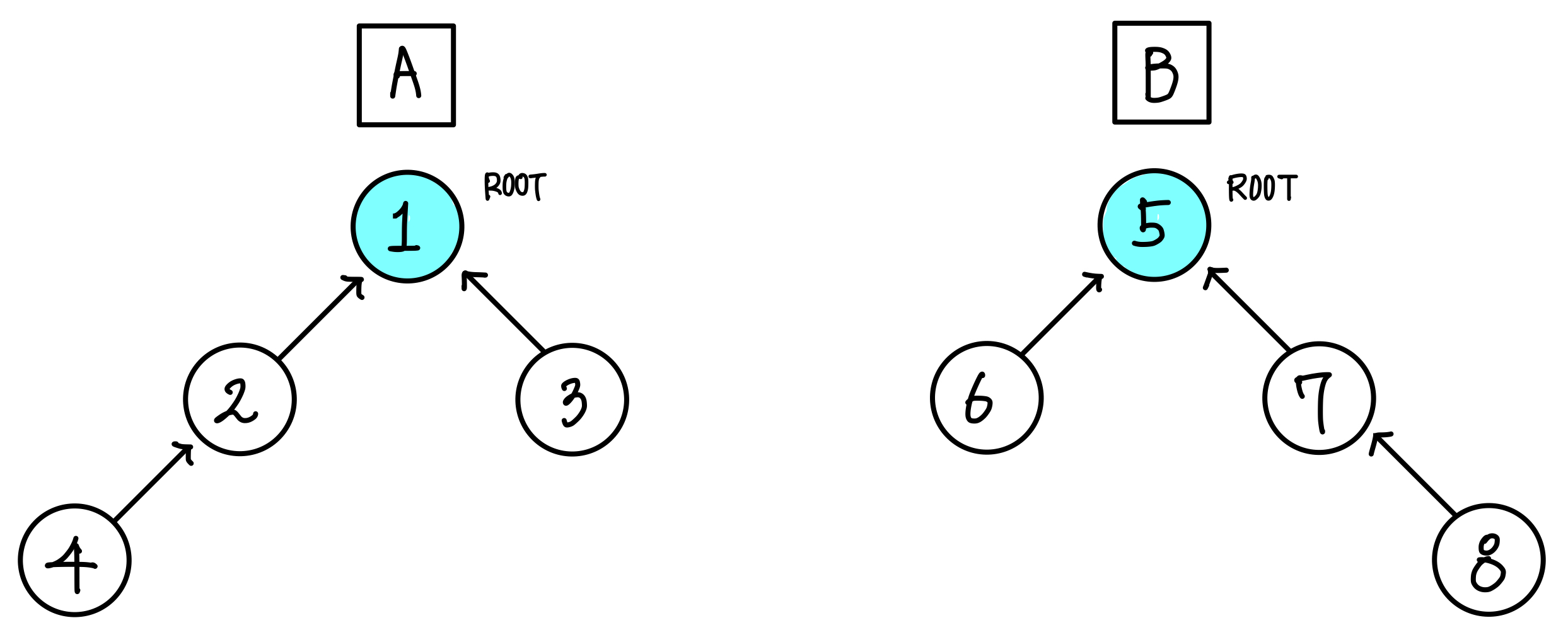
현재 A와 B는 서로소 집합이기 때문에 합 연산(Union)을 할 수 있다.
일단은 A를 B에 합한다고 해보자.
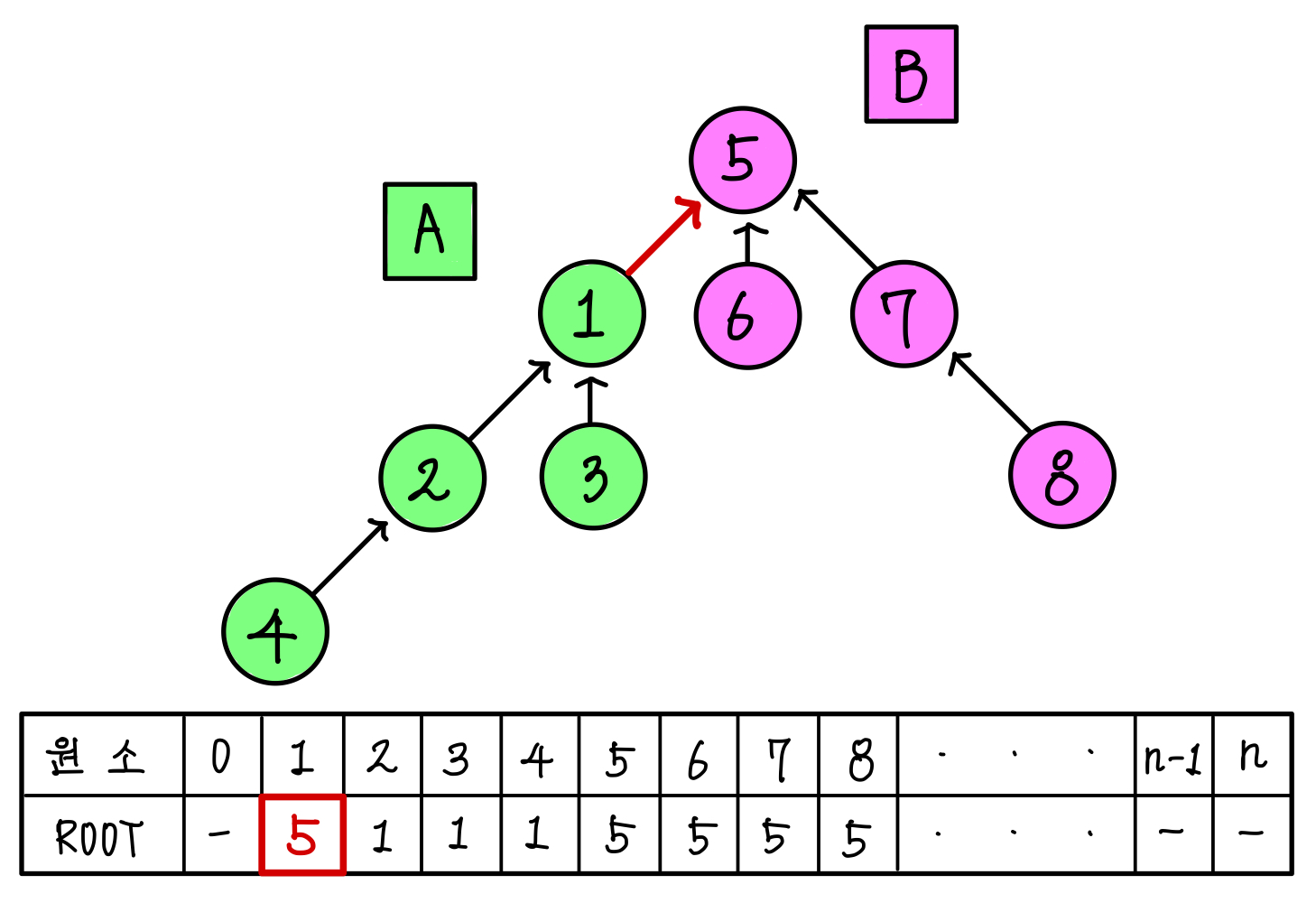
배열이었다면 A의 모든 원소들을 B에 옮겨줘야하지만, 트리로 되어있어서 A의 루트 노드를 B의 루트 노드에 이어주면 된다.▼
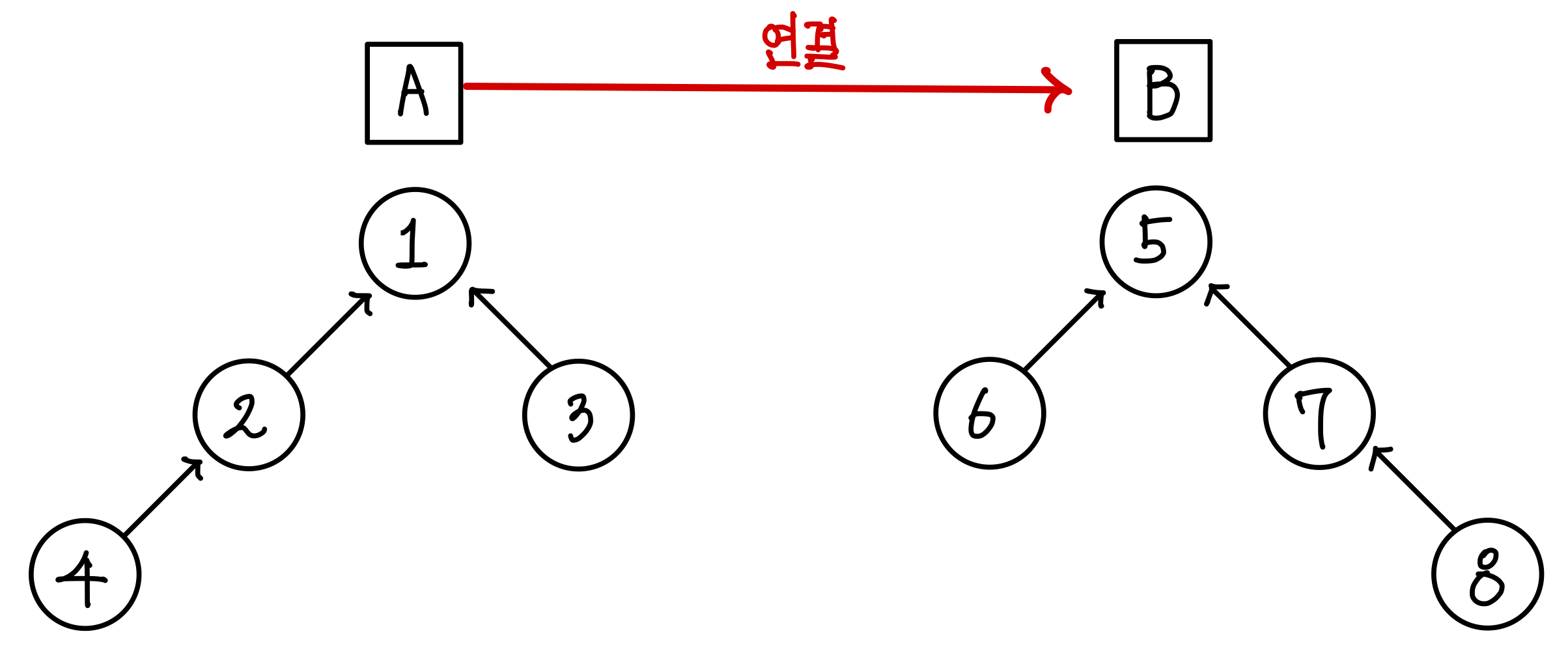
이를 조금 더 보기 좋게 정리하면 아래의 그림처럼 된다.▼
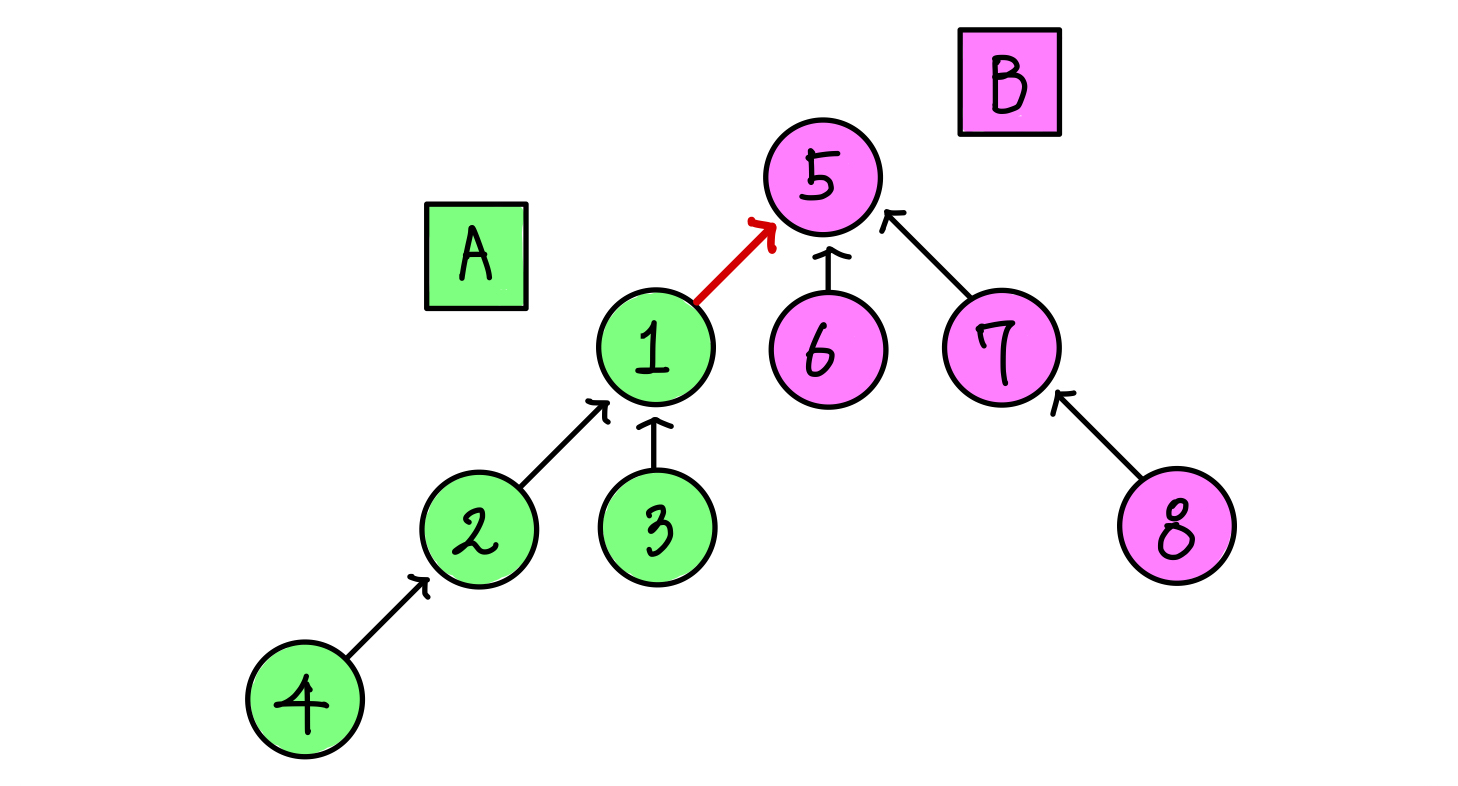
둘은 서로소라는걸 가정하고 합쳤기 때문에, 단순히 루트 노드를 이어줌으로써 합연산을 할 수 있다.
이를 배열의 값으로 보면 아래와 같이 된다.▼
코드
void make_union(int a, int b) {
int pa = find_parent(a);
int pb = find_parent(b);
if (pa > pb)
parent[pa] = pb;
else if (pa < pb)
parent[pb] = pa;
}
최적화
위의 Union-Find 알고리즘이 어떻게 동작하는 지 알겠고 훌륭한 알고리즘인 것도 알았는데, 문제가 있다.
Union 함수를 실행시켰는데, 아래의 그림과 같이 연결이 되면 Find 함수에서 재귀함수를 여러 번 돌려야한다.▼
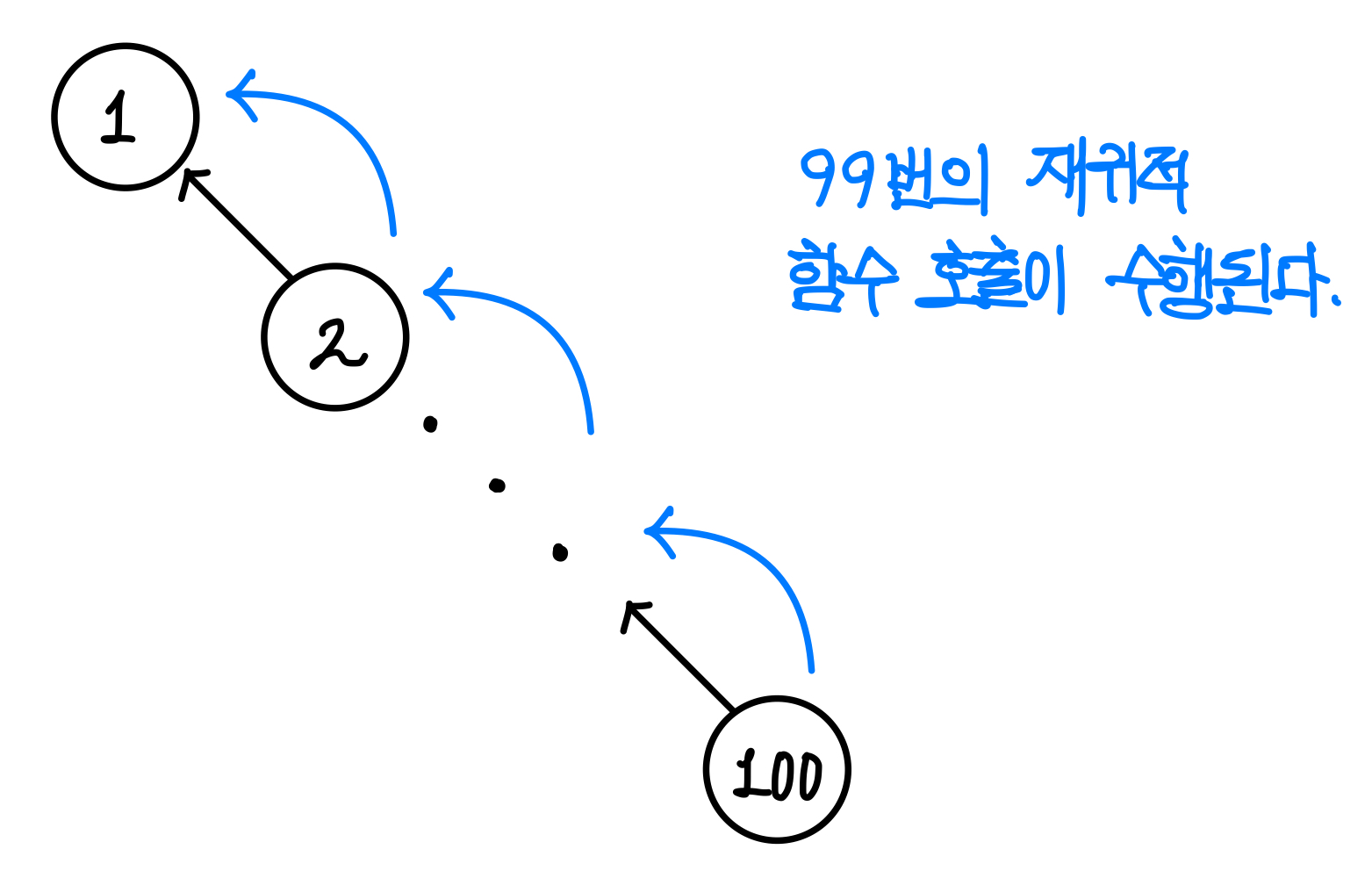
재귀함수를 이렇게 많이 돌리면 시간이 오래걸리므로 비효율적이다.
그래서 최적화 작업이 필요하며, 최적화에는 Find와 Union에 각각 하나씩 총 두 가지가 존재한다.
경로 압축
첫번째 최적화인 경로 압축은 Find 연산에서 수행된다.
Find 연산을 할 때 마다 루트 노드에 하위 노드들을 붙여주는 연산을 해주면 재귀 횟수를 줄일 수 있다. ▼
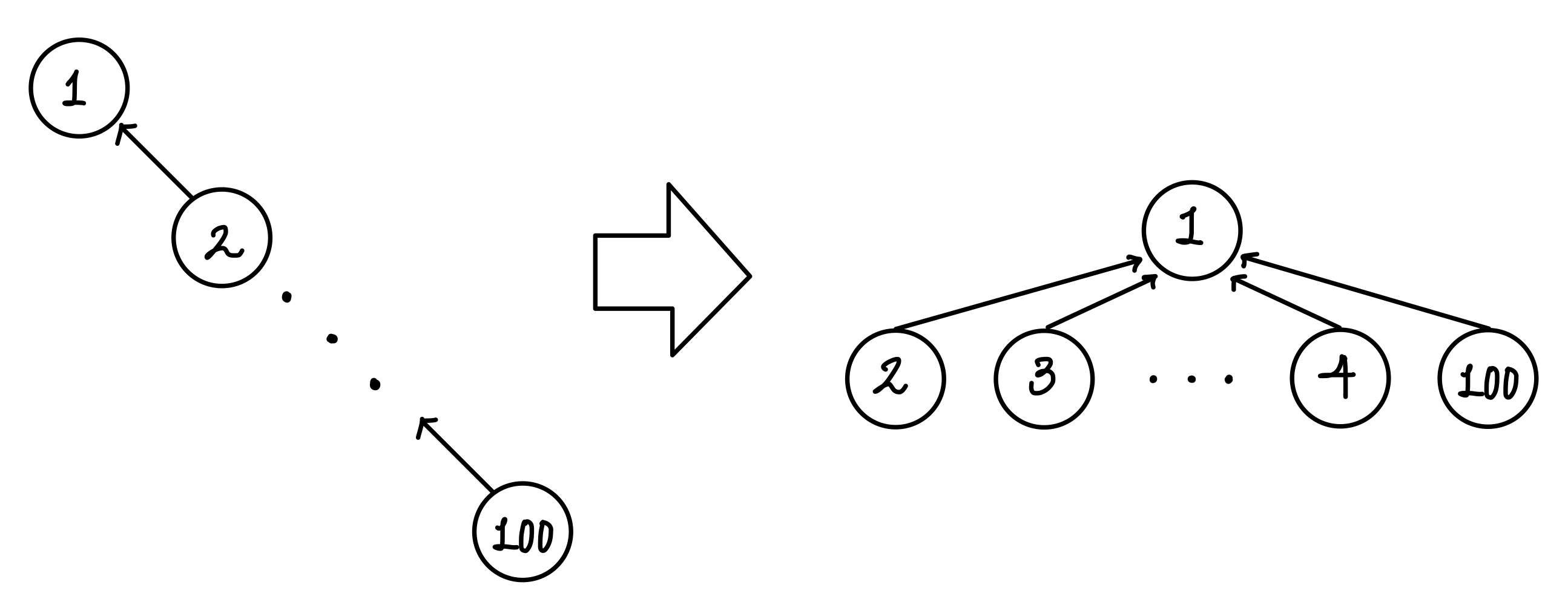
코드
이 과정은 Find에서 한 코드만 넣어주면 된다. ▼
int find_parent(int a) {
if (a == parent[a])
return a;
else
return parent[a] = find_parent(parent[a]);
}
작은 집합을 큰 집합에 붙이기
두번째 최적화는 Union 연산에서 수행된다.
작은 집합을 큰 집합에 붙이는 굉장히 간단한 최적화이다.
별 거 없어보이지만 이 과정을 통해 트리의 높이를 줄일 수 있고, 높이가 줄어듦으로써 재귀 횟수를 줄일 수 있다.
아래의 트리가 있다고 해보자. ▼
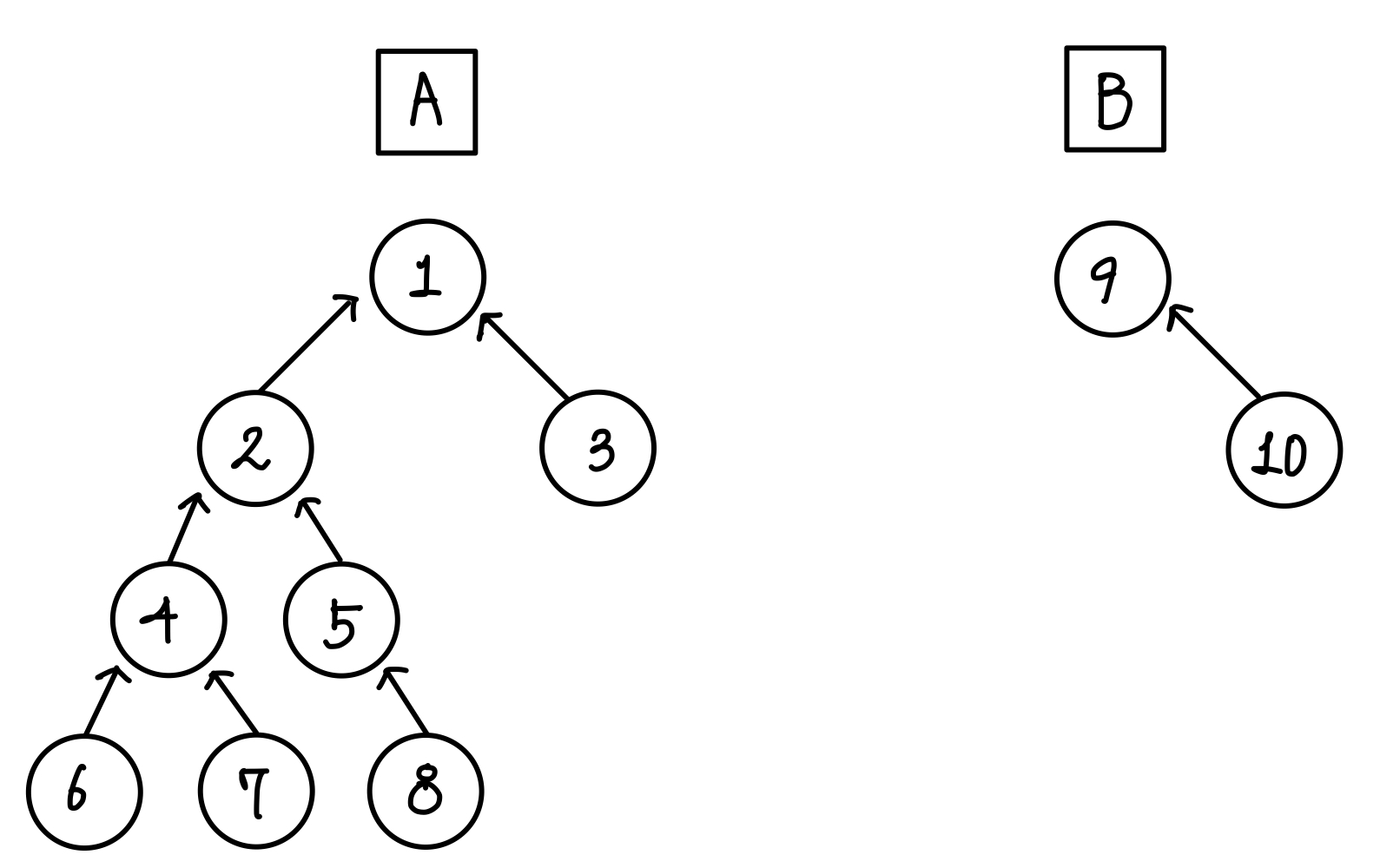
둘을 Union 한다고 했을 때, A를 B에 붙이는 것과 B를 A에 붙이는 것의 결과는 다르게 나온다. ▼
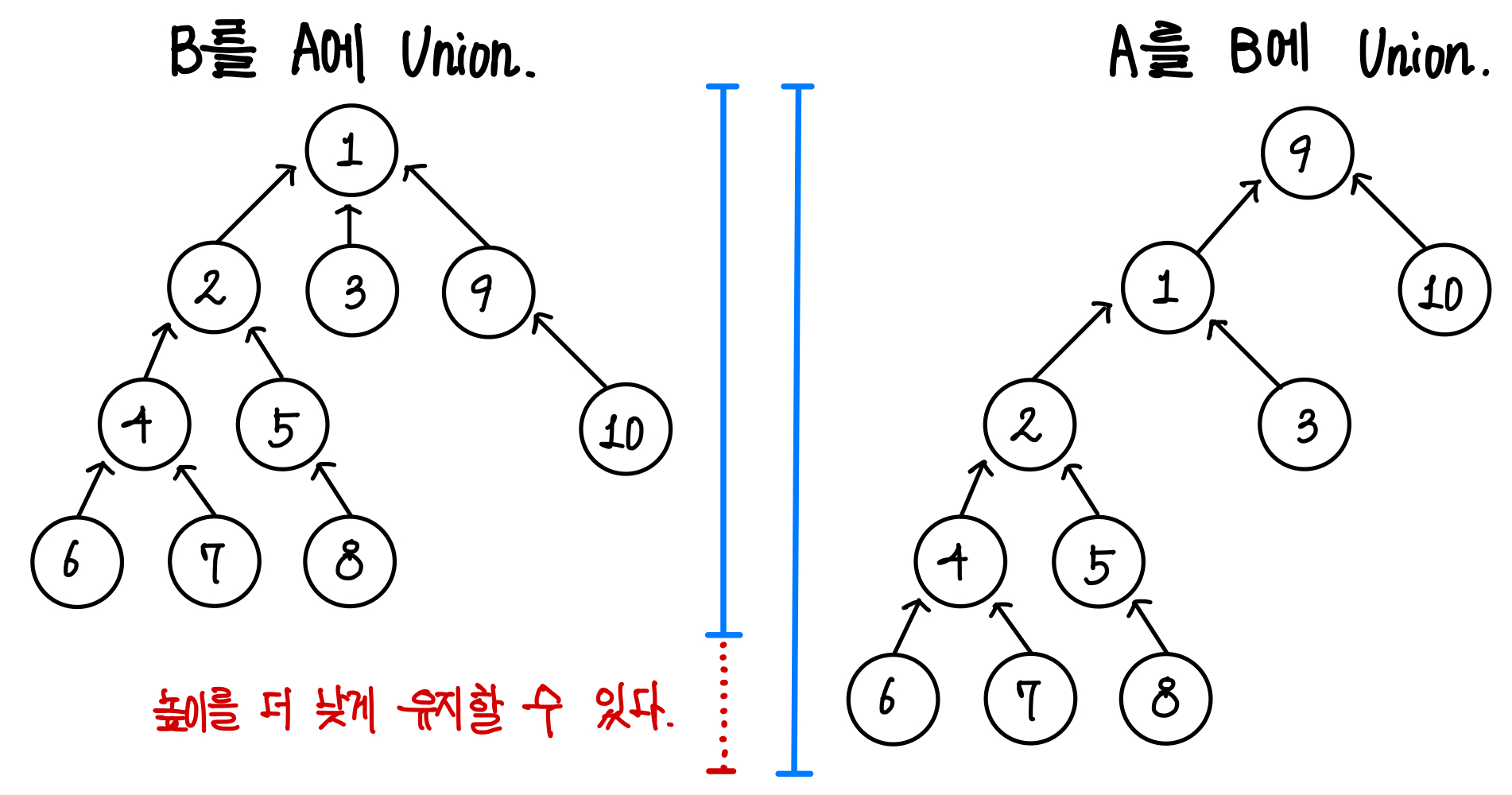
이렇게 작은 집합(B)을 큰 집합(A)에 붙이는 것 만으로도 트리의 높이를 더 낮게 유지할 수 있다.
코드
void make_union(int a, int b) {
int pa = find_parent(a);
int pb = find_parent(b);
if(size(pa) < size(pb)){
parent[pa] = pb;
} else {
parent[pb] = pa;
}
}'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 플로이드 와샬 (0) | 2024.02.15 |
|---|---|
| 벨만 포드 (0) | 2024.02.15 |
| 다익스트라 (0) | 2024.02.13 |
| MST, 최소 신장 트리 (0) | 2024.02.08 |
| 그래프와 그래프 탐색 (0) | 2024.02.07 |




