

개요
간단하게 말하면, 최소 신장 트리란 신장 트리 중에서 사용된 가중치 합이 최소인 트리를 말한다.
신장 트리란? (Spanning Tree)
신장 트리란, 그래프 내의 모든 정점을 포함하는 트리를 말한다.
스패닝 트리, 신장 트리, Spanning Tree 모두 같은 말이다.
신장 트리는 그래프의 최소 연결 부분 그래프를 말한다.
여기서 최소 연결이라고 하면, 간선의 수가 가장 작은 것을 말한다.
n개의 정점을 가지는 그래프의 최소 간선의 수는 n - 1 개이고, n - 1 개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 되며 이를 신장 트리라고 부른다.
한 그래프에는 아래 그림처럼 여러 개의 신장 트리가 있을 수 있다.
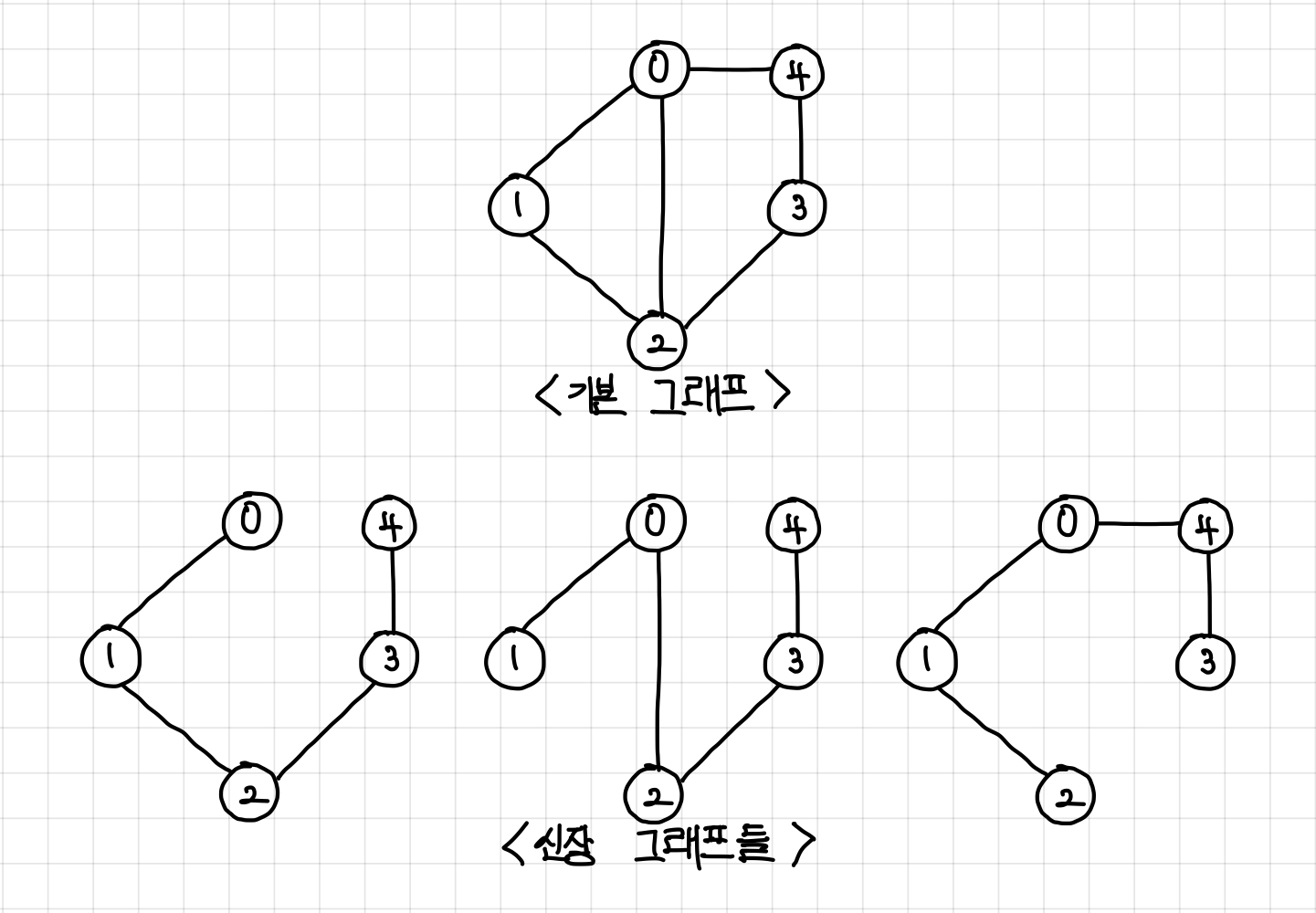
결국, 최소 신장 트리란
최소 연결된 부분 그래프들 중 간선 가중치의 합이 가장 적은 트리를 말한다.
이 말은 즉, 한 그래프에서 나올 수 있는 모든 신장 그래프들 중 간선 가중치 합이 가장 작은 신장 그래프라는 것이다.
특징을 조금 보면, 아래의 특징을 갖는다.
- 나올 수 있는 모든 신장 그래프들 중 간선의 가중치의 합이 최소.
n개의 정점을 가지는 그래프는n - 1개의 간선만을 사용.- 사이클은 포함되서는 안됨.
(3번의 경우, 1번과 2번 조건이 만족된다면 만족될 리 없는 특징이다.)
최소 신장 트리의 구현 방법
최소 신장 트리를 구현하는 방법으로는 두가지가 존재한다.
- Kruskal MST 알고리즘
- Prim MST 알고리즘
Kruskal 알고리즘의 경우 그리디 알고리즘을 이용하여 최적 해답을 구하는 방식이고,
Prim 알고리즘의 경우 단계적 확장 방식을 이용하여 최적 해답을 구하는 방식이다.
Kruskal MST 알고리즘
Kruskal 알고리즘은 그리디 알고리즘을 이용하여 그래프의 모든 간선을 최소 비용으로 연결하는 최적 해를 구하는 방식을 말한다.
그리디 알고리즘은 그 순간에는 최적이지만, 최종 해답이 최적이라는 보장이 없다는 단점이 있다.
하지만 Kruskal 알고리즘은 최적의 해답을 도출할 수 있다는 것으로 증명되었다.
알고리즘 동작
- 그래프의 간선들의 가중치를 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 싸이클을 형성하지 않는 간선을 선택한다.
가장 낮은 가중치를 먼저 선택하고, 싸이클을 형성하는 간선은 제외한다.
싸이클이 발생하는지의 여부는 Union-Find 알고리즘을 적용하면 된다. - 해당 간선을 MST의 집합에 추가한다.
동작 과정
1. 이런 식으로 그래프가 있다고 해보자.
이를 먼저 오름차순으로 정렬한다.
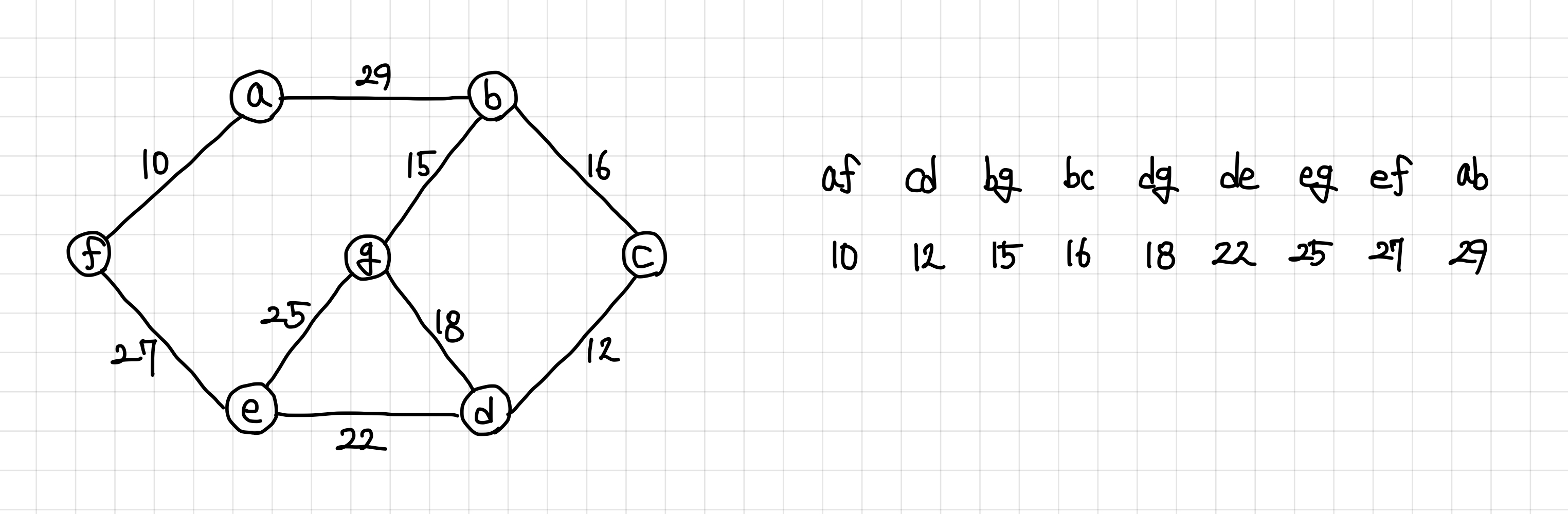
2. 그리고 가장 앞에 와있는 간선부터 하나씩 MST 집합에 추가해본다.
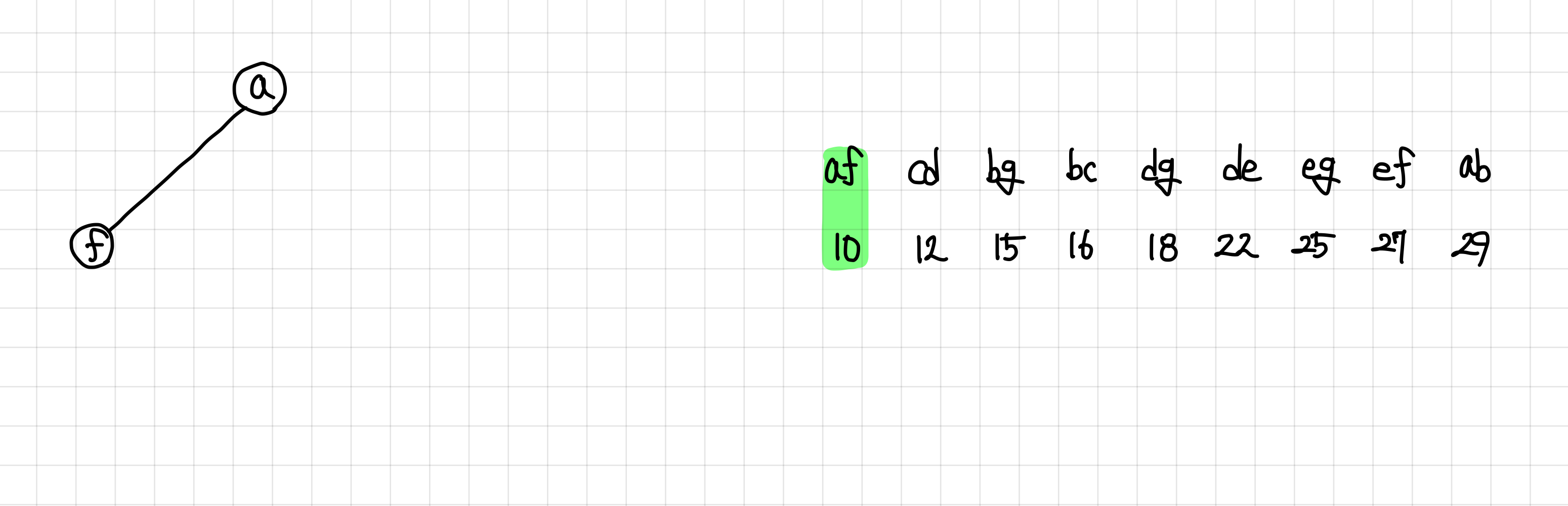
3. 차례차례 간선을 확인해본다.
앞의 간선과는 연결되진 않지만, 싸이클이 형성되진 않으므로 MST 집합에 추가한다.
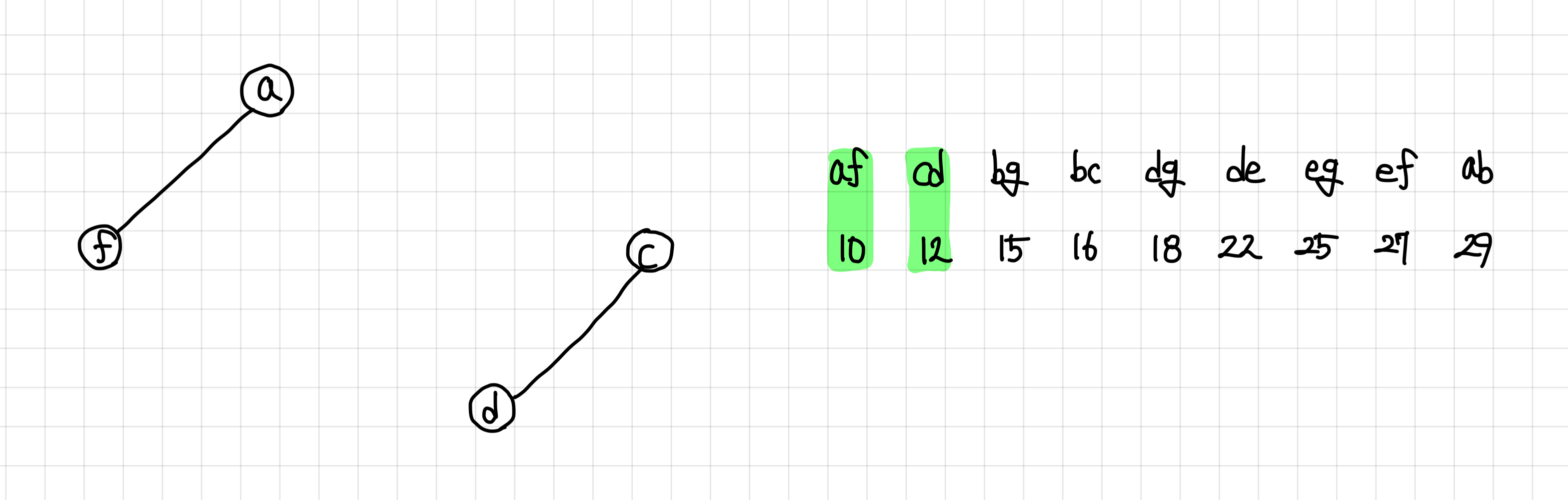
4. 다음 간선도 확인해본다.
여전히 연결되진 않지만, 싸이클이 형성되진 않으므로 MST 집합에 추가한다.
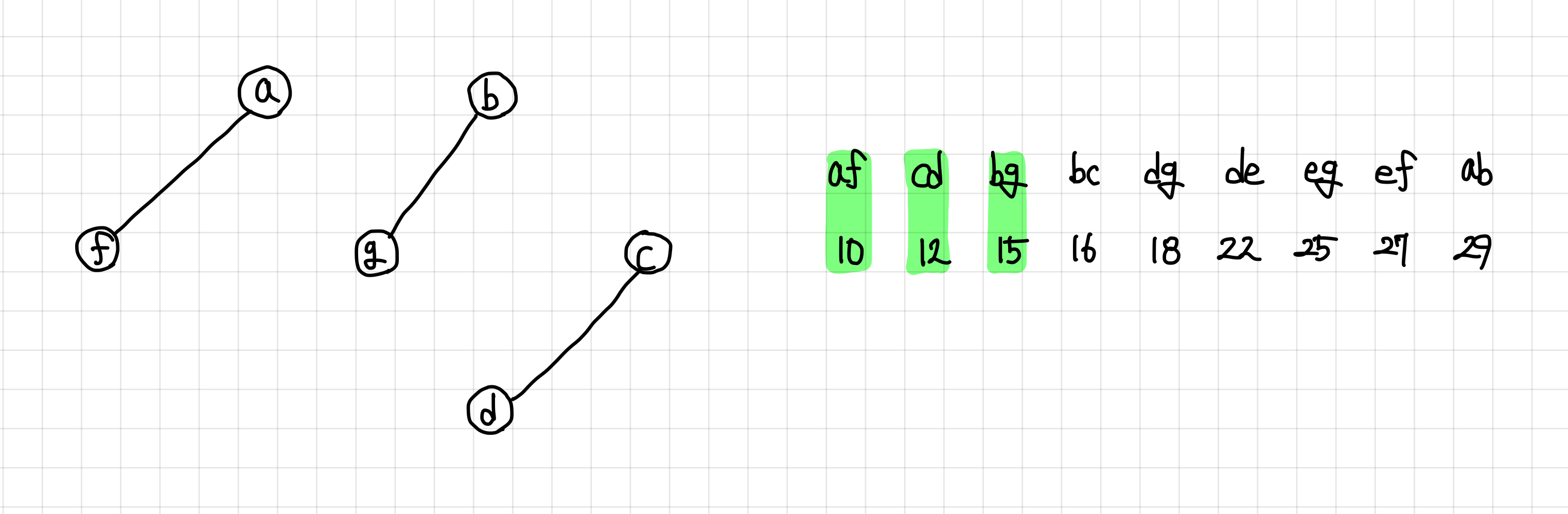
5. 다음 간선은 연결이 된다. 연결은 됐지만, 싸이클은 형성하지 않으므로 MST 집합에 추가한다.
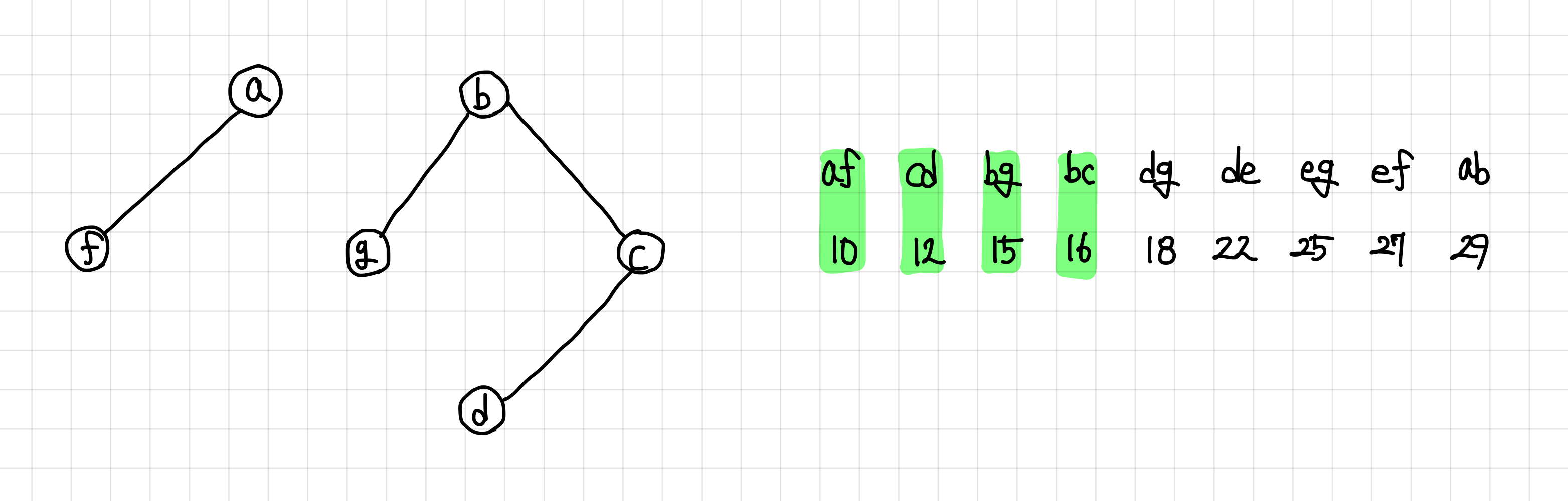
6. 다음 간선도 연결은 된다.
하지만 싸이클을 형성하므로 MST 집합에 추가하지 않는다.
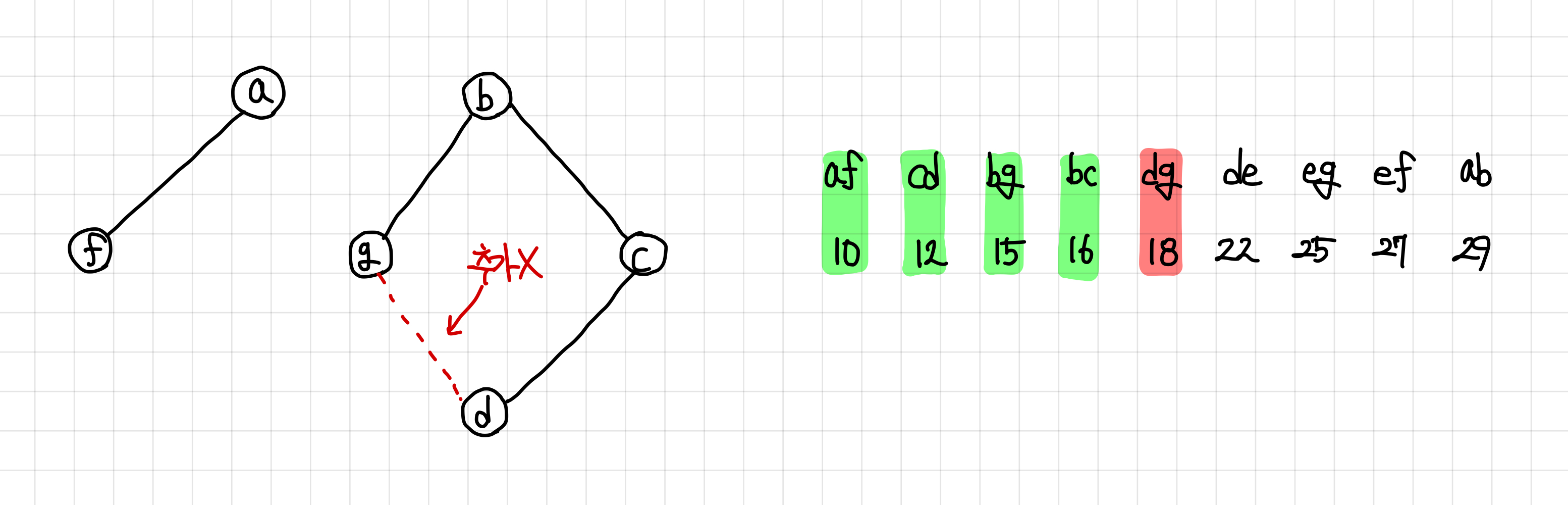
7. 똑같이, 연결은 되지만 싸이클은 형성하지 않으므로 MST 집합에 추가해준다.
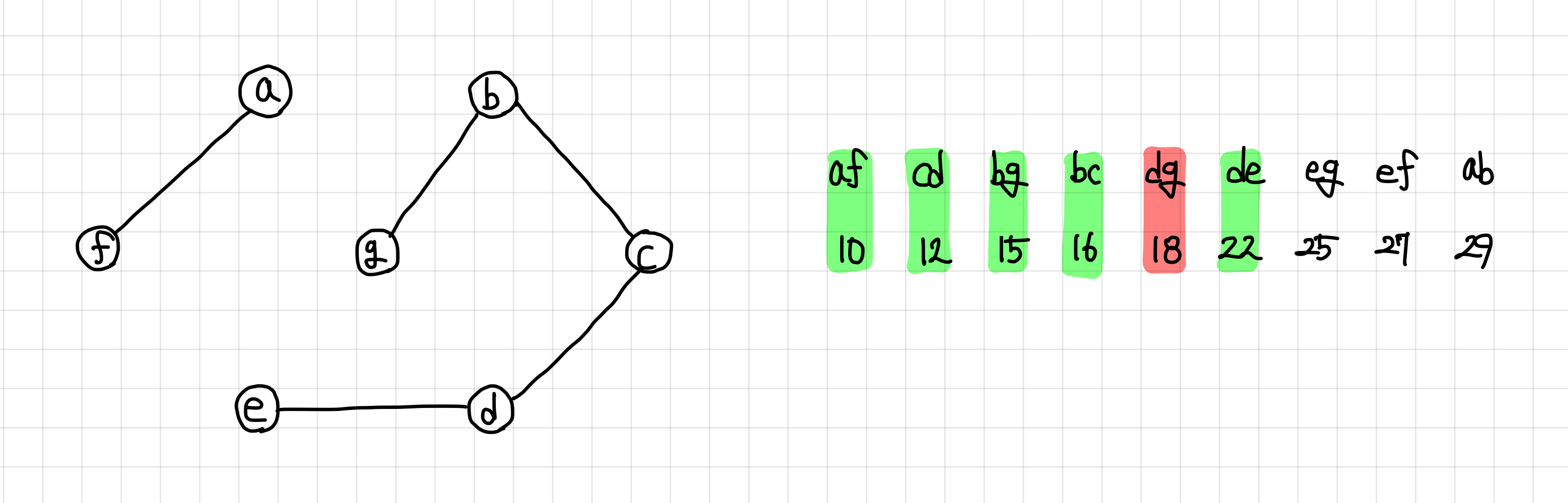
8. 다음 간선은 연결되면서 싸이클을 형성하기에 MST 집합에 추가하지 않는다.
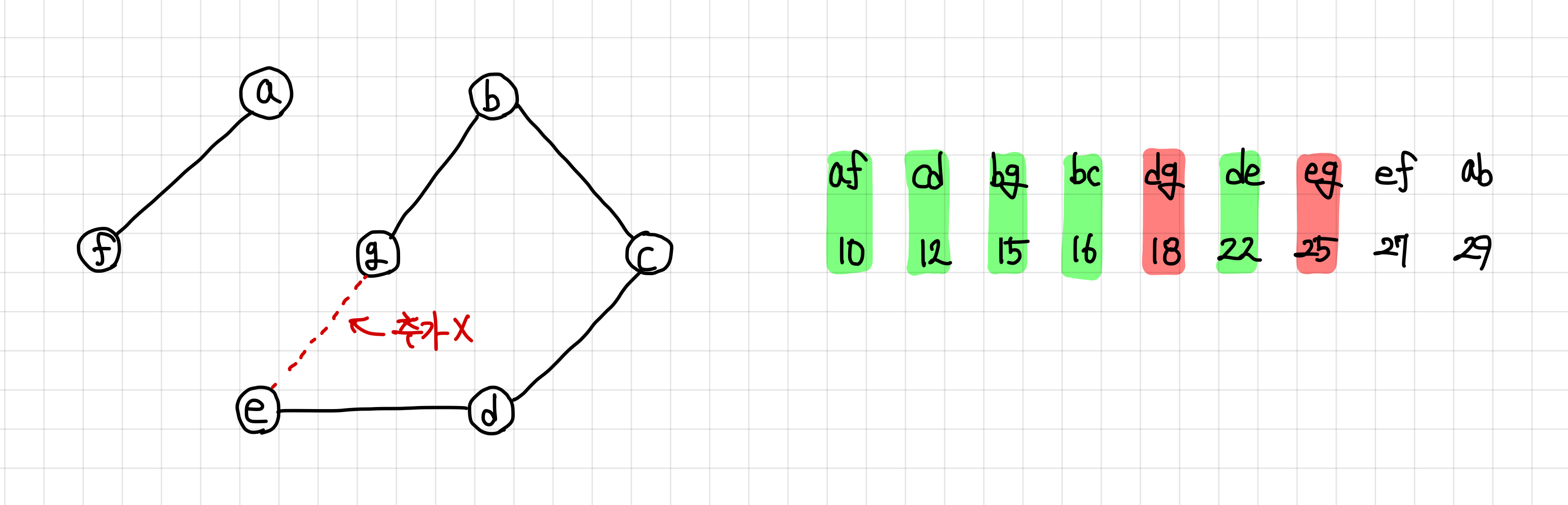
9. 다음 간선은 연결이 되고, 싸이클도 형성하지 않으므로 MST 집합에 추가한다.
MST 집합에 이 간선을 추가하면, `n - 1`개를 만족하므로 종료해도 된다. 하지만 일단 마지막 간선까지 보겠다.
당연하게도, 마지막 간선은 연결하게 되면 싸이클을 형성하므로 추가하지 않는다.
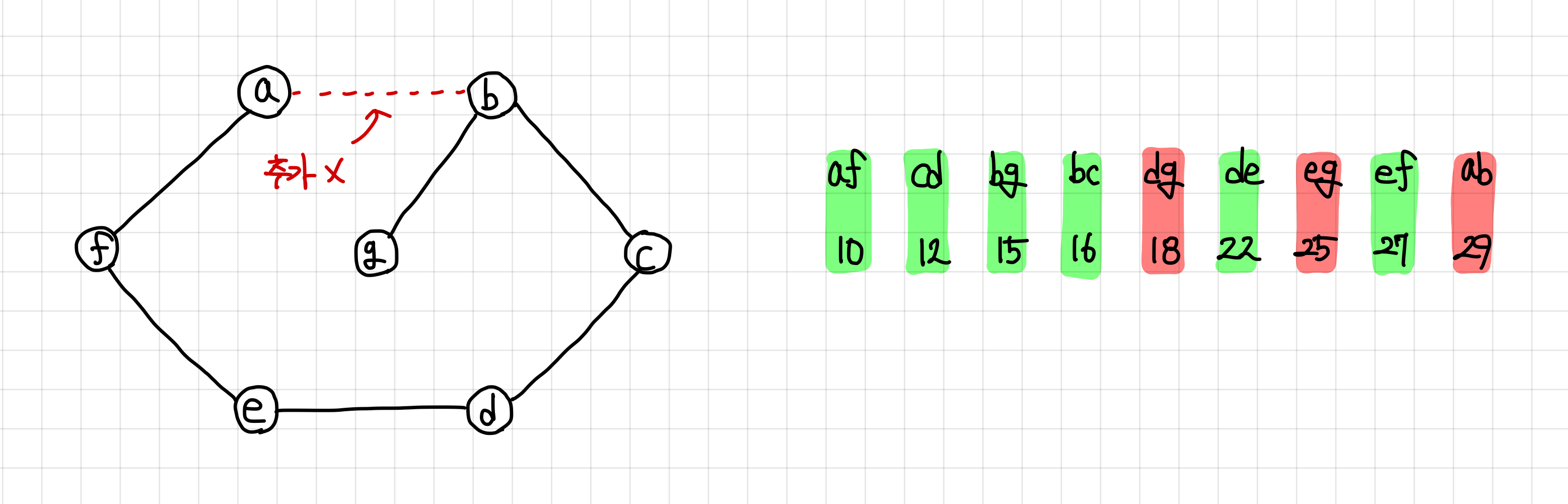
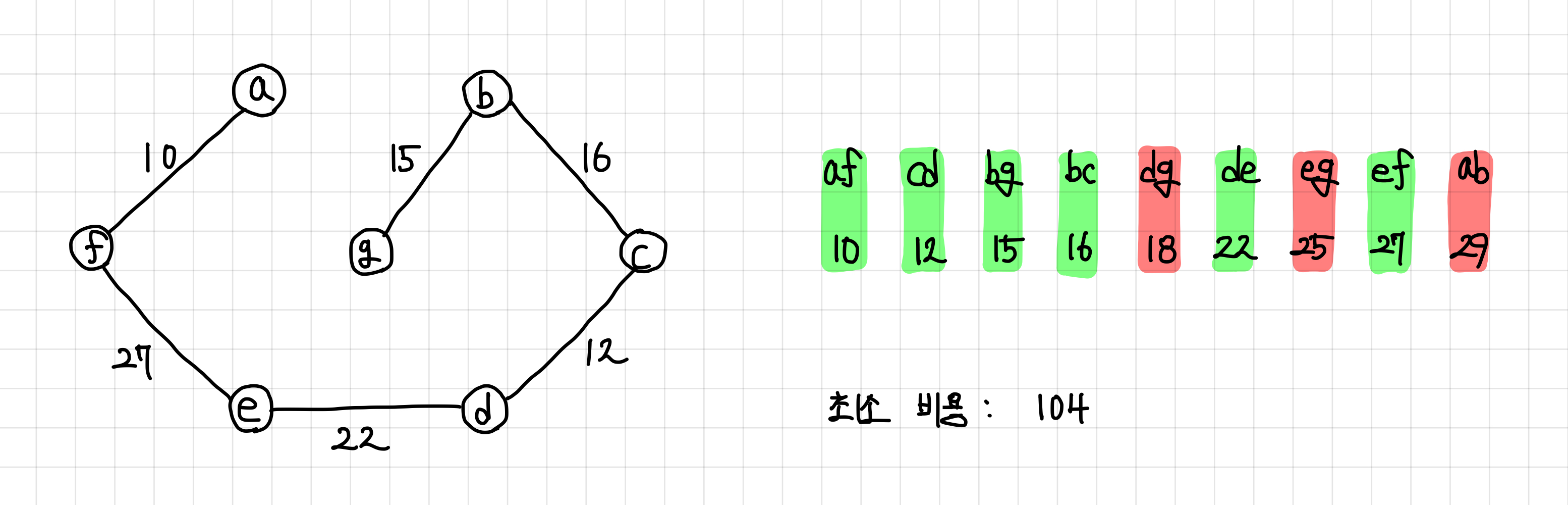
10. 이렇게 마지막 간선까지 확인하게 되면, 최소 신장 트리의 정보를 얻을 수 있게 된다.
의사 코드
function Kruskal(G)
for each vertex v in G do
Define an elementary cluster C(v) ← {v}.
Initialize a priority queue Q to contain all edges in G, using the weights as keys.
Define a tree T ← Ø //T will ultimately contain the edges of the MST
// n is total number of vertices
while T has fewer than n-1 edge
시간 복잡도
정렬 알고리즘의 시간 복잡도를 O(ElogV)라고 하자. (E는 간선 개수, V는 정점 개수)
모든 정점을 독립적인 집합으로 만드는 과정의 시간 복잡도는 O(V)이다.
마지막으로 Union-Find 기법을 사용하므로, 시간 복잡도는 O(1)이다.
셋을 합쳐주면, 가장 높은 시간 복잡도를 따라가므로 시간 복잡도는 O(ElogV)가 된다.
결국 정렬을 빨리 하면 할 수록 빨라진다고 볼 수 있다.
그러나 union 시간복잡도가 V^2일 때, 전체 시간복잡도는 O(ElogV + V^2)이 된다.
union: O(V^2)
sort edge by increasing weight O(ElogV)
⇒ O(ElogV+ V^2)
Prim MST 알고리즘
Prim 알고리즘은 시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 구성하는 방법을 말한다.
알고리즘 동작
- 시작할 때는 시작 정점만이 MST 집합에 들어간다.
- 앞에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
우선 순위 큐를 이용하여 가장 낮은 가중치부터 확인하면 된다. - 위 과정을 간선 개수가 n - 1가 될 때까지 반복한다.
예시
1. 시작 정점을 하나 잡는다.(어떤 값으로 해도 똑같은 결과가 나오므로 아무거나 골라도 상관 없다.)
그 시작 정점의 값을 0으로 초기화하고, MST 집합에 넣어준다.
나머지 값은 전부 INF(무한)로 초기화한다.
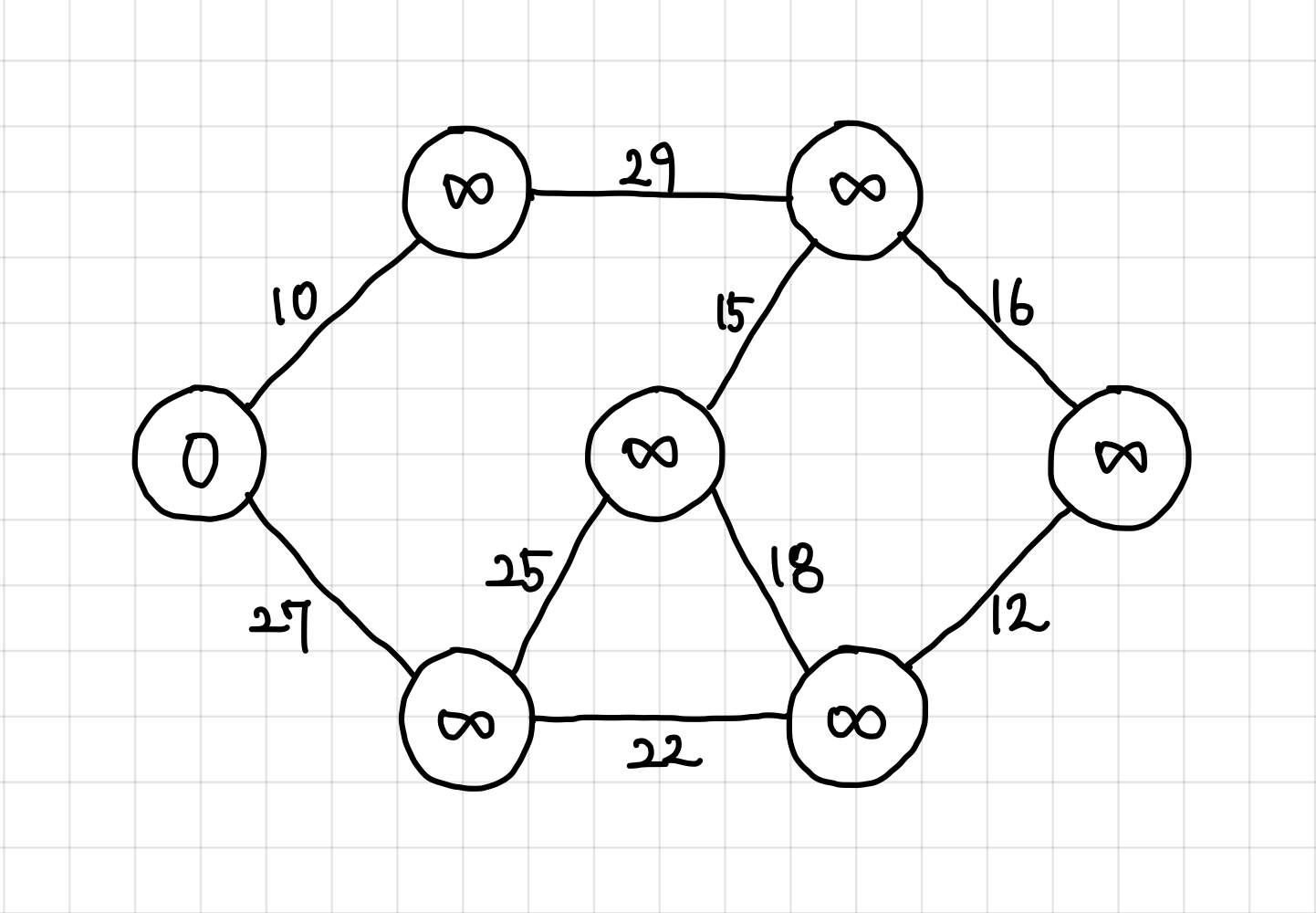
2. MST 집합에 들어간 값의 인접 정점으로 가는 간선을 큐에 넣어준다.
이 때 큐는 우선 순위 큐로, 여기서는 낮은 값이 더 우선이다.
그리고 가장 작은 값을 넣어주면서 값을 갱신하고, 이동한다.
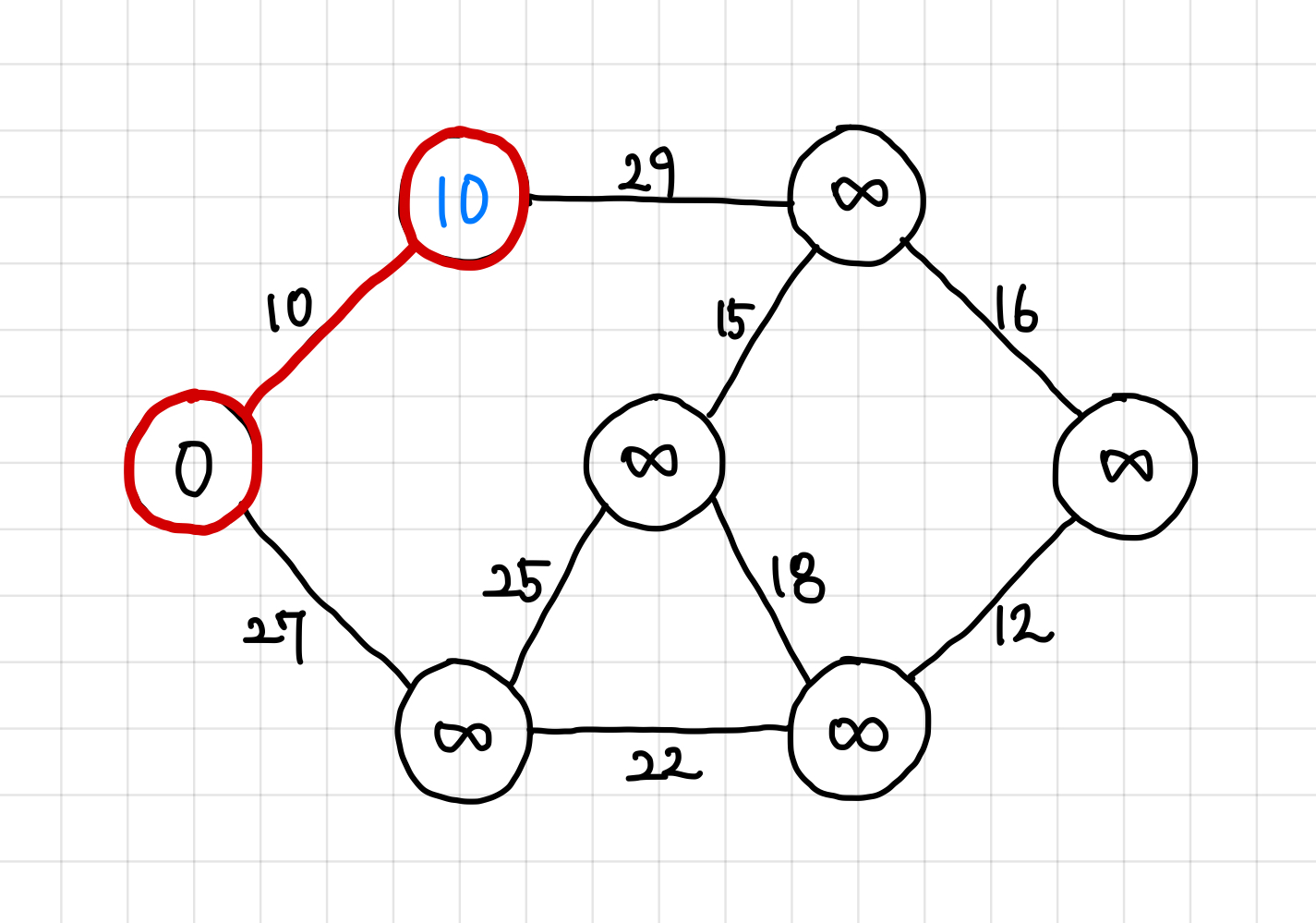
3. 다음 값으로 이동하고, 그 값의 인접 정점으로 가는 간선을 우선 순위 큐에 넣어준다.
현재는 29보다는 27이 더 작으므로, 다음에는 가중치 27짜리 간선을 타고 이동한다.
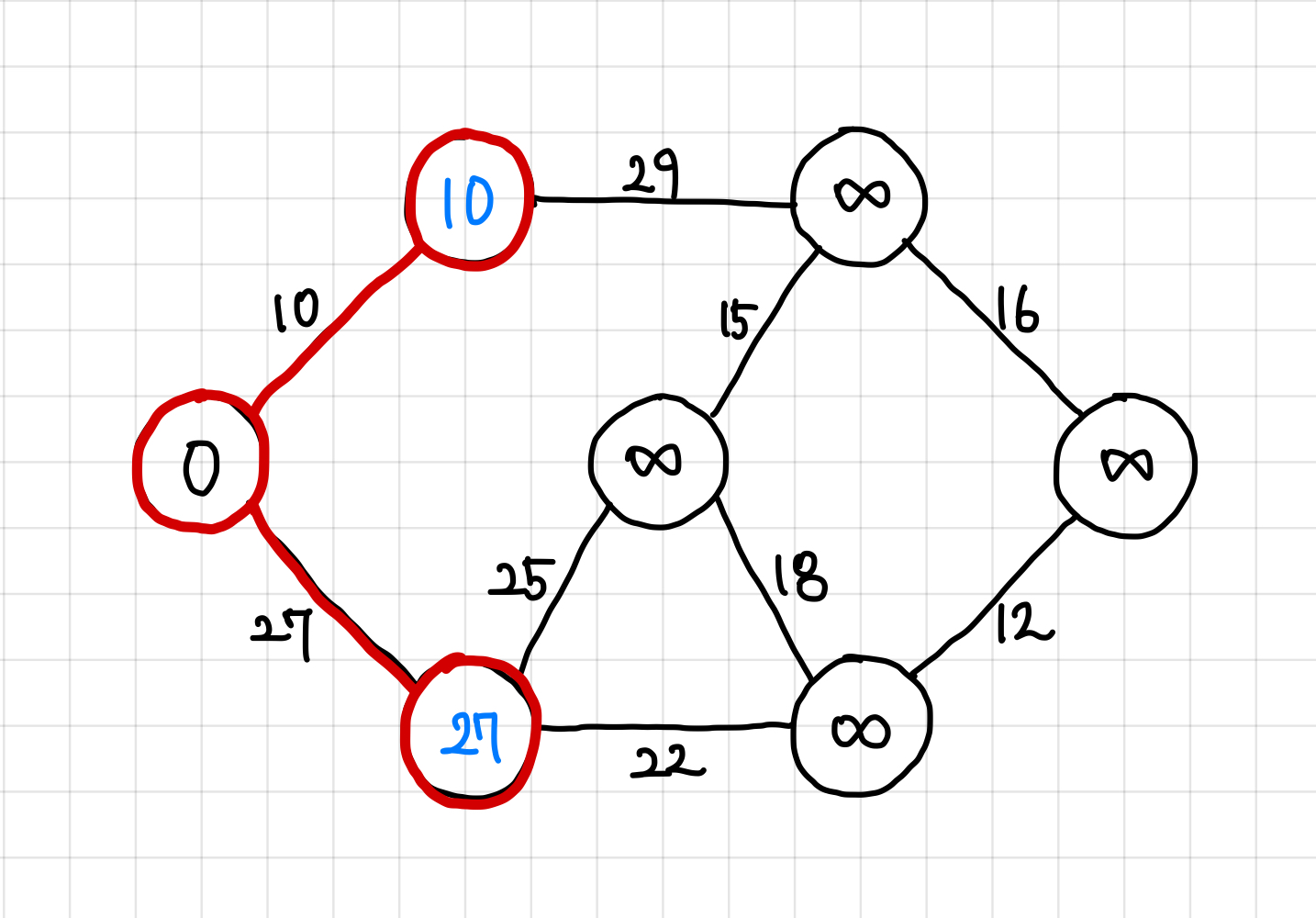
4. 다음 정점으로 이동했을 때, 해당 정점의 인접 간선을 우선 순위 큐에 넣어준다.
25, 22, 29가 큐에 들어있게 되고, 이 중 가장 작은 값인 가중치 22짜리 간선을 타고 이동한다.
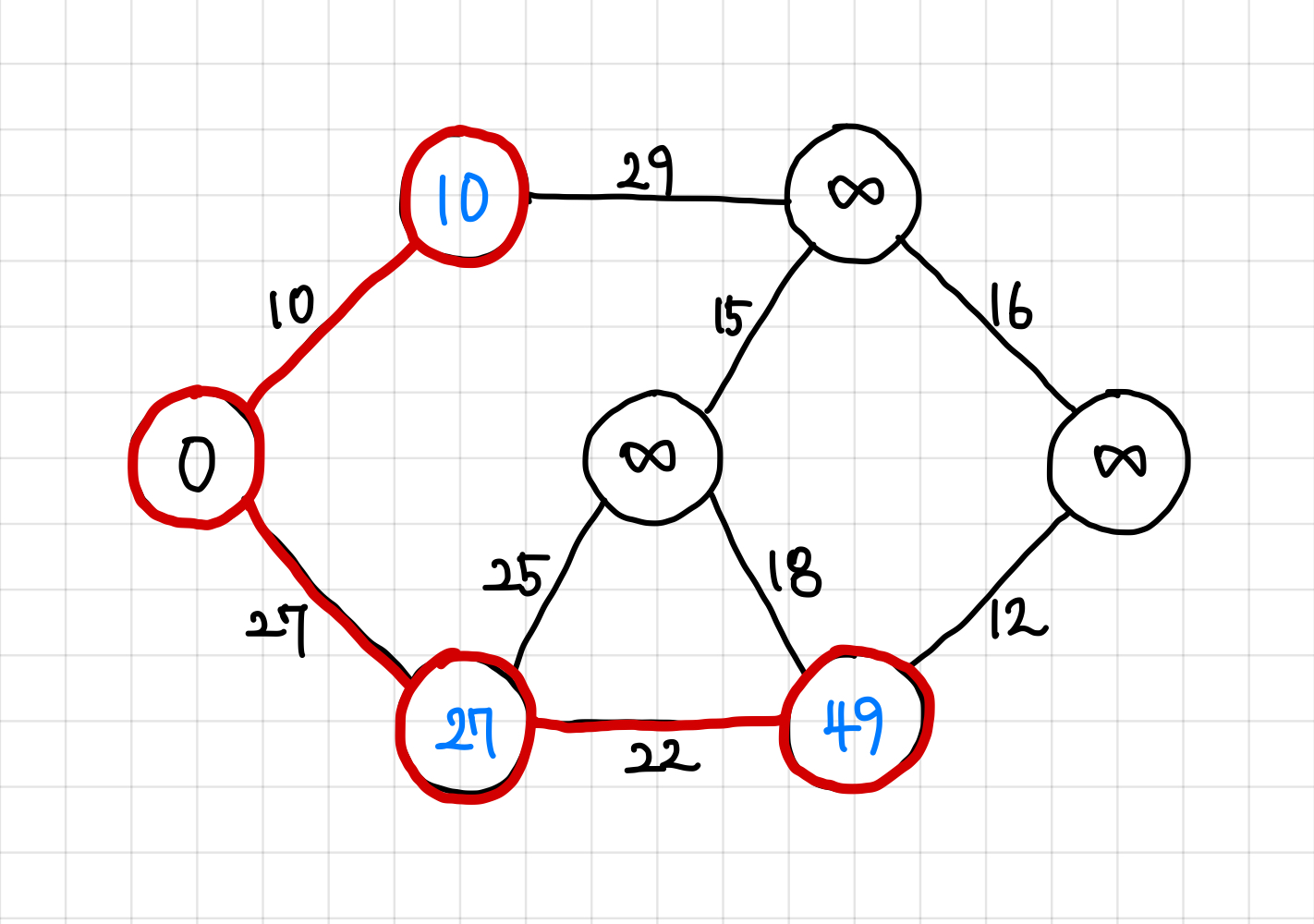
5. 앞에서와 똑같이 큐에 값을 넣어주고, 가장 작은 가중치의 간선으로 이동한다. 현재는 큐에 25, 29, 18, 12가 들어있게 되고 이 중 가장 작은 가중치 12짜리 간선으로 이동한다.
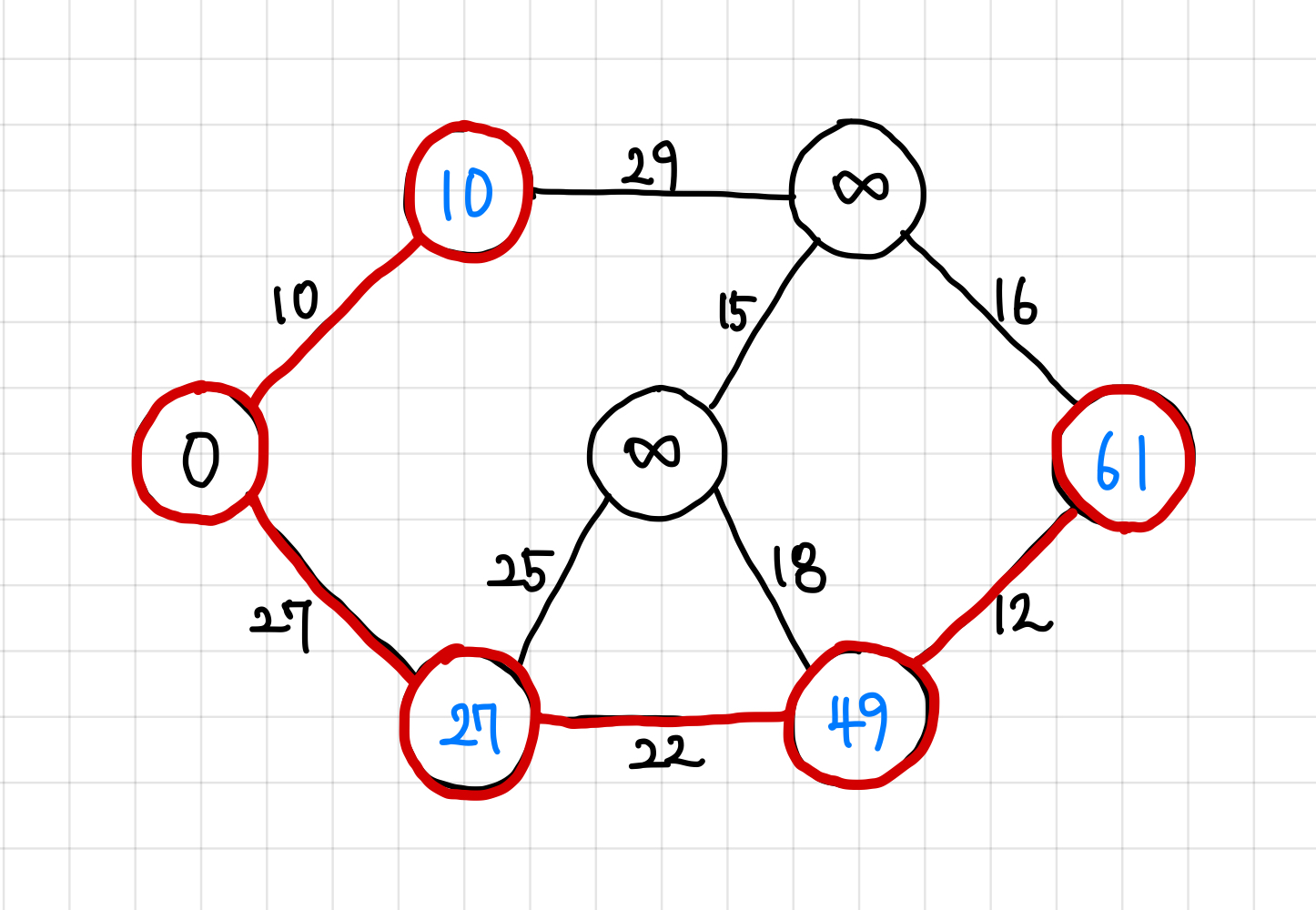
6. 인접 간선 값을 큐에 넣어주고, 똑같이 가장 작은 값의 간선으로 이동한다.
큐에는 25, 29, 18, 16이 들어있고, 이 중 가장 작은 16으로 이동한다.
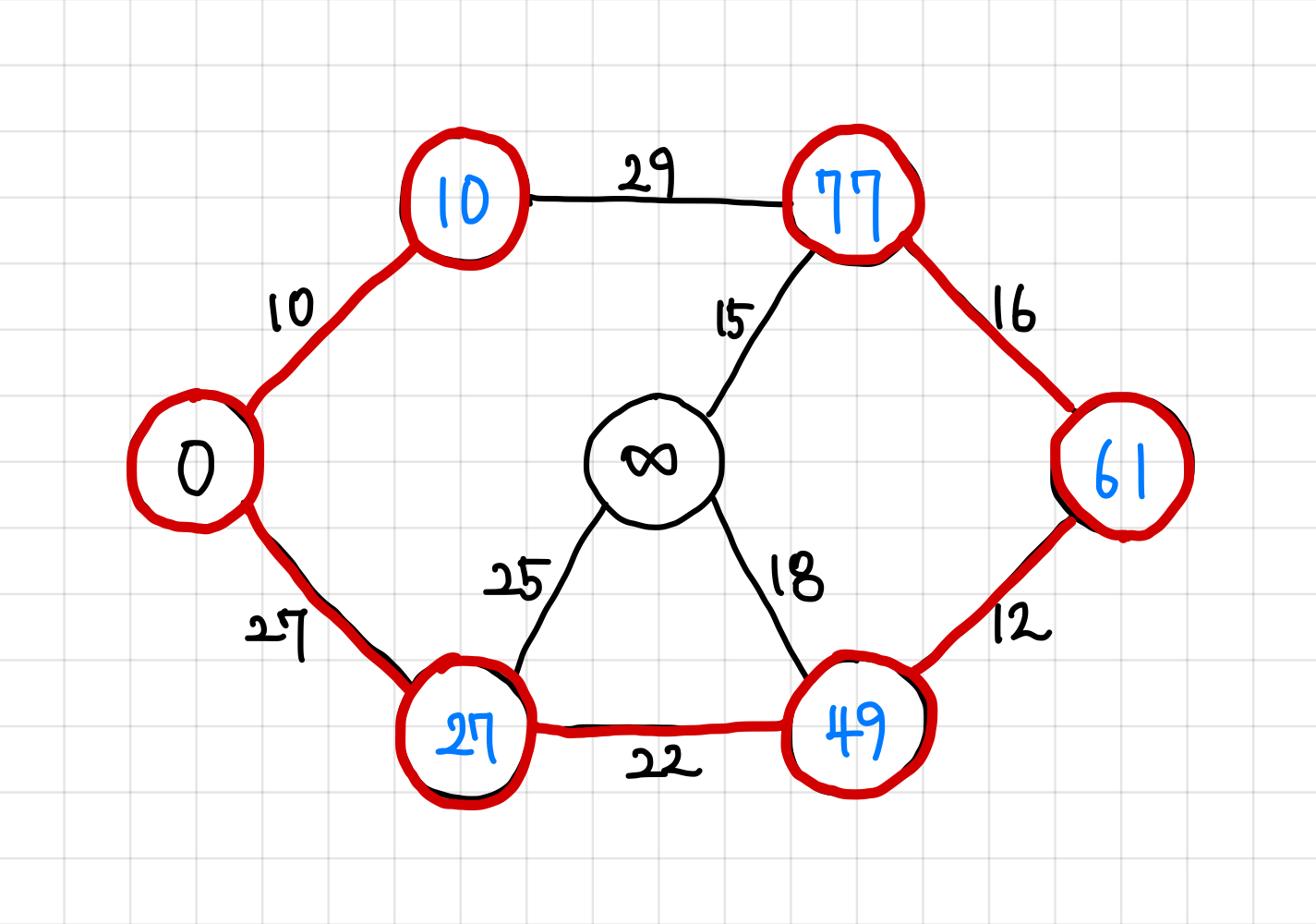
7. 인접 간선 값을 큐에 넣어준다.
29는 이미 포함된 값이므로 넣지 않고, 15만 넣어준다.
큐에는 25, 29, 18, 15가 들어있게 되고, 이 중 가장 작은 15로 이동한다.
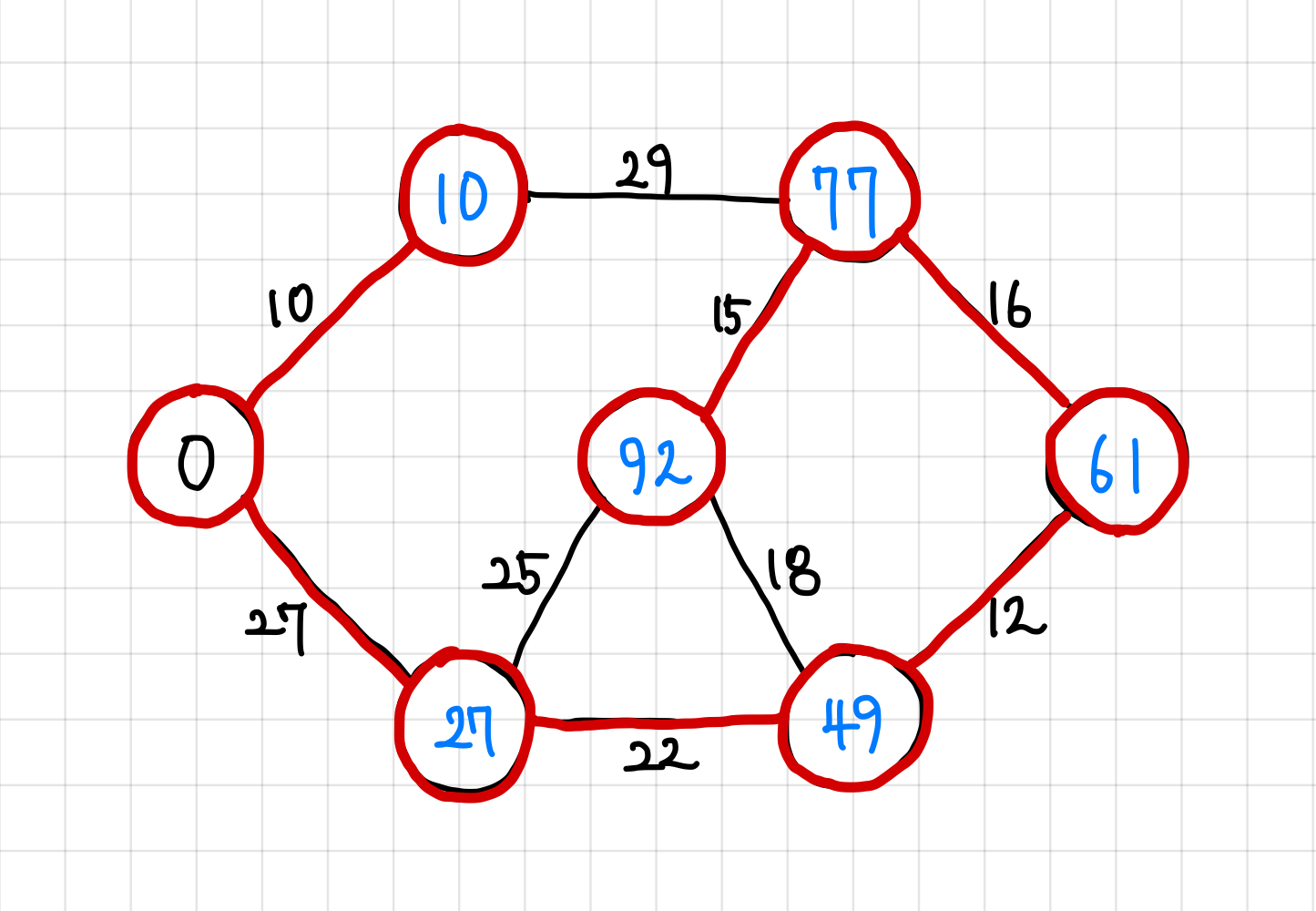
8. 이렇게 `n - 1`개의 간선이 MST 집합에 들어가게 됐으므로, 종료한다. 혹시 싸이클이 형성됐을 수도 있으니, 모든 정점을 다 연결했는지 정점의 값들이 INF인지 아닌지 확인해본다.모두 INF가 아니므로, 해당 MST 집합이 최적해가 된다.
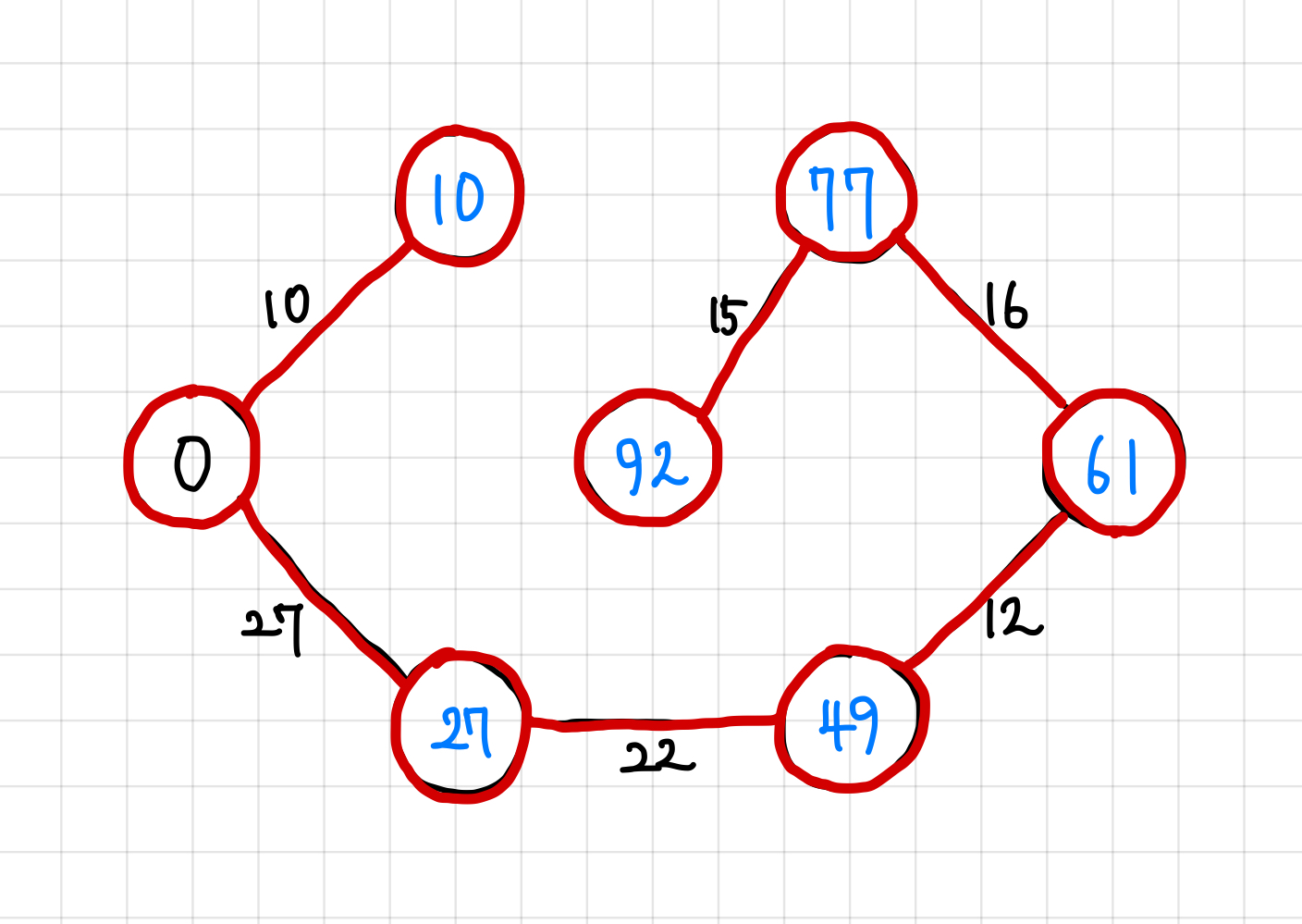
의사 코드
for each vertex in graph
set min_distance of vertex to ∞
set parent of vertex to null
set minimum_adjacency_list of vertex to empty list
set is_in_Q of vertex to true
set distance of initial vertex to zero
add to minimum-heap Q all vertices in graph.
while latest_addition = remove minimum in Q
set is_in_Q of latest_addition to false
add latest_addition to (minimum_adjacency_list of (parent of latest_addition))
add (parent of latest_addition) to (minimum_adjacency_list of latest_addition)
for each adjacent of latest_addition
if (is_in_Q of adjacent) and (weight-function(latest_addition, adjacent) < min_distance of adjacent)
set parent of adjacent to latest_addition
set min_distance of adjacent to weight-function(latest_addition, adjacent)
update adjacent in Q, order by min_distance
시간 복잡도
mark: n번
for each unmarked neighbor w of v: 2m번
while(e←pop()): 최대 m번
O(n+mlogn)
Prim과 Kruskal 둘 중 더 나은 것은?
둘의 시간 복잡도를 보면,
Kruskal은 O(ElogE)
Prim은 O(V^2)
임을 알 수 있다.
얼추 보면 Prim의 시간복잡도가 V^2이라서, 더 오래걸리는 것 처럼 보이지만,
둘의 시간 복잡도는 서로 다른 것을 기준으로 정해졌다.
Kruskal은 간선의 개수가 기준이고, Prim은 정점의 개수가 기준이다.
그래서 둘을 비교하는 것은 별로 의미가 없는 행위이다.
그래프 내에서 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph)의 경우 Kruskal이,
그래프 내에서 간선이 많이 존재하는 밀집 그래프(Dense Graph)의 경우는 Prim이 더 적합하다.
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 벨만 포드 (0) | 2024.02.15 |
|---|---|
| 다익스트라 (0) | 2024.02.13 |
| 그래프와 그래프 탐색 (0) | 2024.02.07 |
| 다이나믹 프로그래밍 (0) | 2024.02.07 |
| 분할 정복 (0) | 2024.01.27 |




