

개요
가중치가 있는 그래프에서 최단 경로 문제를 푸는 알고리즘이다.
최단 경로 문제라고 하면 다익스트라와 같은 작업을 수행하고, 심지어는 다익스트라가 더 빠르기까지 하다.
하지만 벨만-포드 알고리즘의 의의는 다익스트라 알고리즘이 처리하지 못하는 음수인 간선을 처리할 수 있다는 것이다.
그래서 음수인 간선이 등장하는 경우에는 벨만-포드 알고리즘을 사용한다.
알고리즘
벨만-포드 알고리즘에서 중요한 부분
벨만-포드 알고리즘에서 가장 중요시 해야할 부분은 음의 싸이클이다.
벨만-포드 알고리즘은 다익스트라 알고리즘과 같이 값이 더 작은 값이 나오면 갱신하는 식으로 진행된다.
그런데 음의 싸이클이 등장하게 되면, 한 번 순회를 돌 때마다 값이 계속 작아져서 무한히 갱신하게 된다.
그래서 우리는 순회 횟수를 V - 1로 제한을 한다. (여기서 V는 정점 개수다.)
왜냐하면 시작 정점에서 특정 정점까지 도달하기 위해 거쳐가는 최대 간선 수는 V - 1 개이기 때문이다.
따라서 경로에 V번째 간선이 추가되면 싸이클에 진입했다고 판단한다.
그러면 본격적으로 동작을 보자.
알고리즘 동작
벨만-포드 알고리즘은 edge relaxion의 반복이라고 할 수 있다.
edge relaxion 이란?
탐색을 했을 때, 거리가 더 짧아질 수 있다면, 노드와 엣지의 정보를 업데이트하는 것을 말한다.
- 그래프 초기화
- relax 반복
- 음의 간선이 있는 지 체크
동작 예시
왼쪽은 간선이 표시된 그래프이고, 오른쪽은 최단 거리를 표시할 그래프이다.
1. 1번 부터 시작할 것이므로, 1번 정점의 최단 거리는 0으로 두고 나머지 정점은 INF로 초기화해준다. ▼
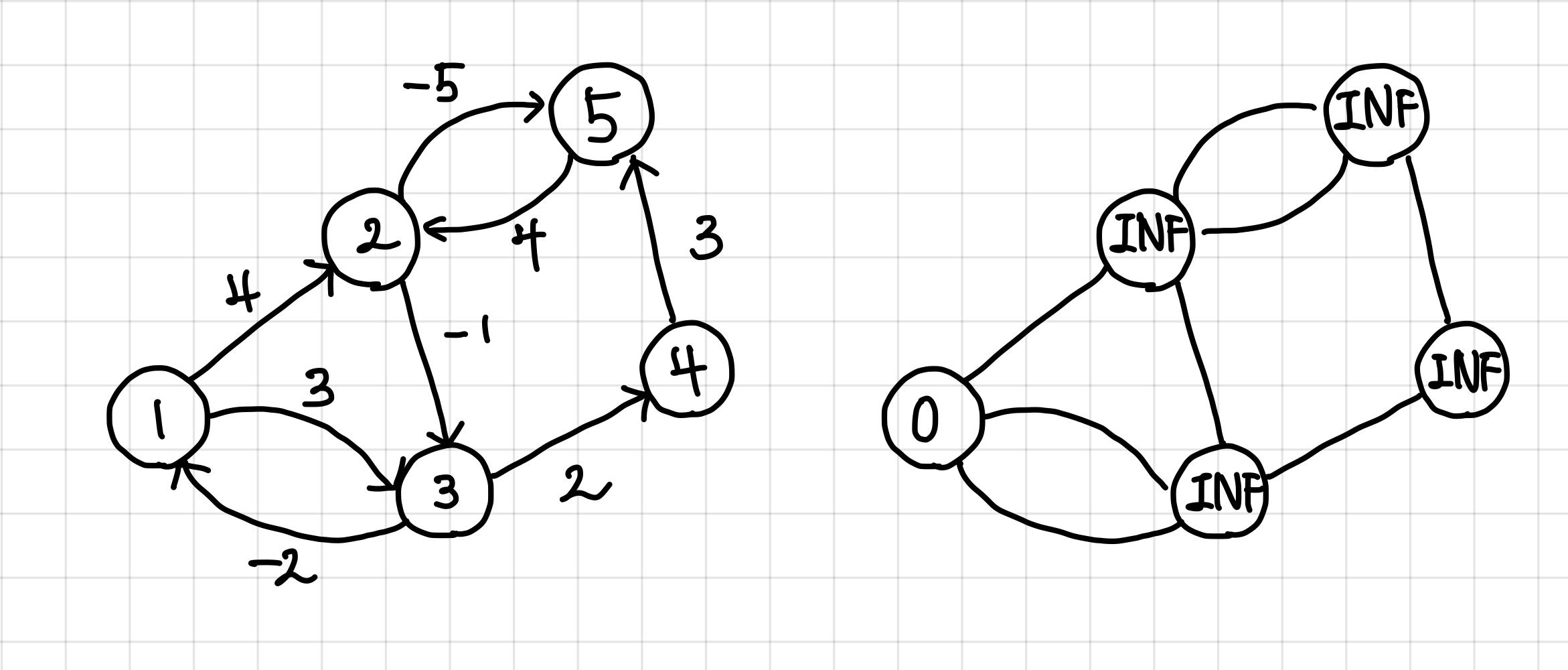
2. 1번 노드부터 모든 간선을 체크해본다.
1번에서 2번으로 간다고 했을 때, 2번 노드에 할당된 값이 INF보다 0 + 4가 더 작으므로 갱신해준다. ▼
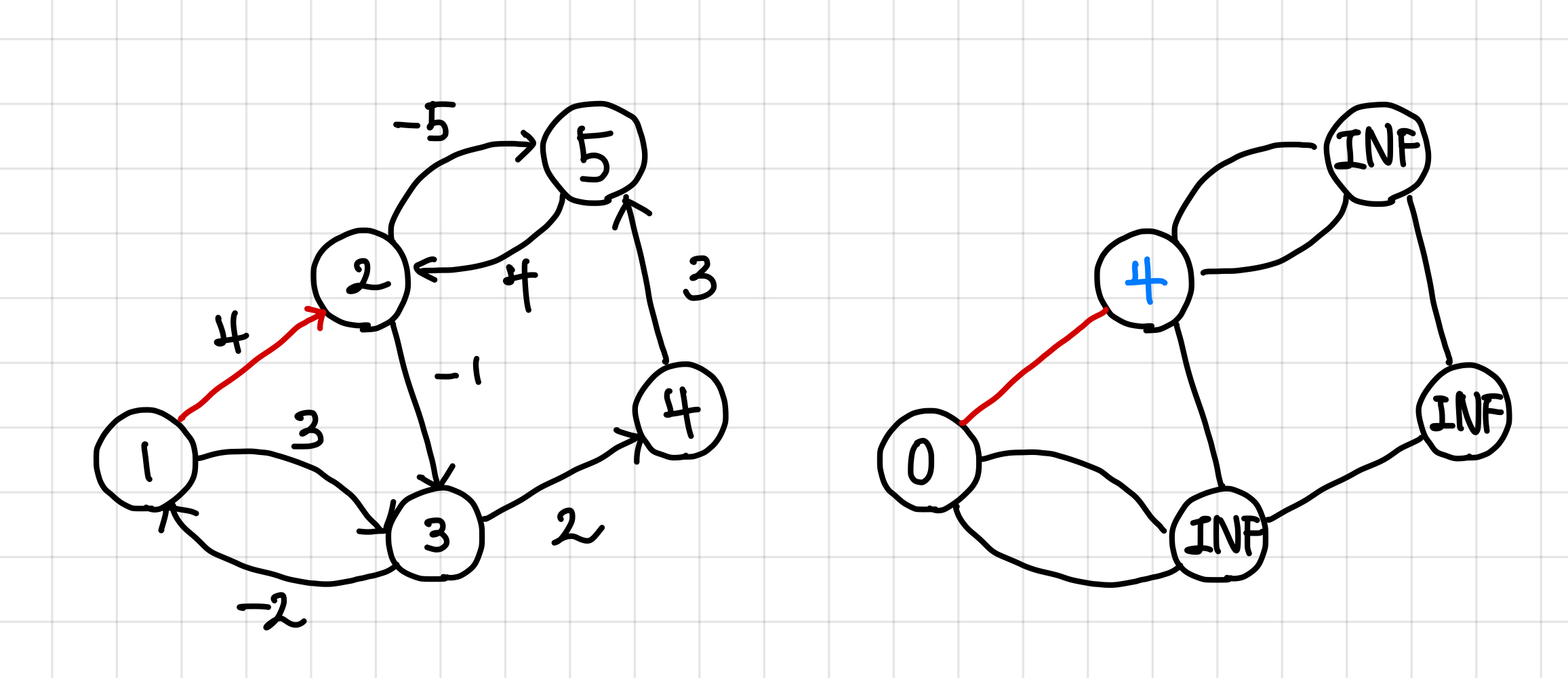
1번에서 3번으로 간다고 했을 때, 3번 노드에 할당된 값이 INF보다 0 + 3이 더 작으므로 갱신해준다. ▼
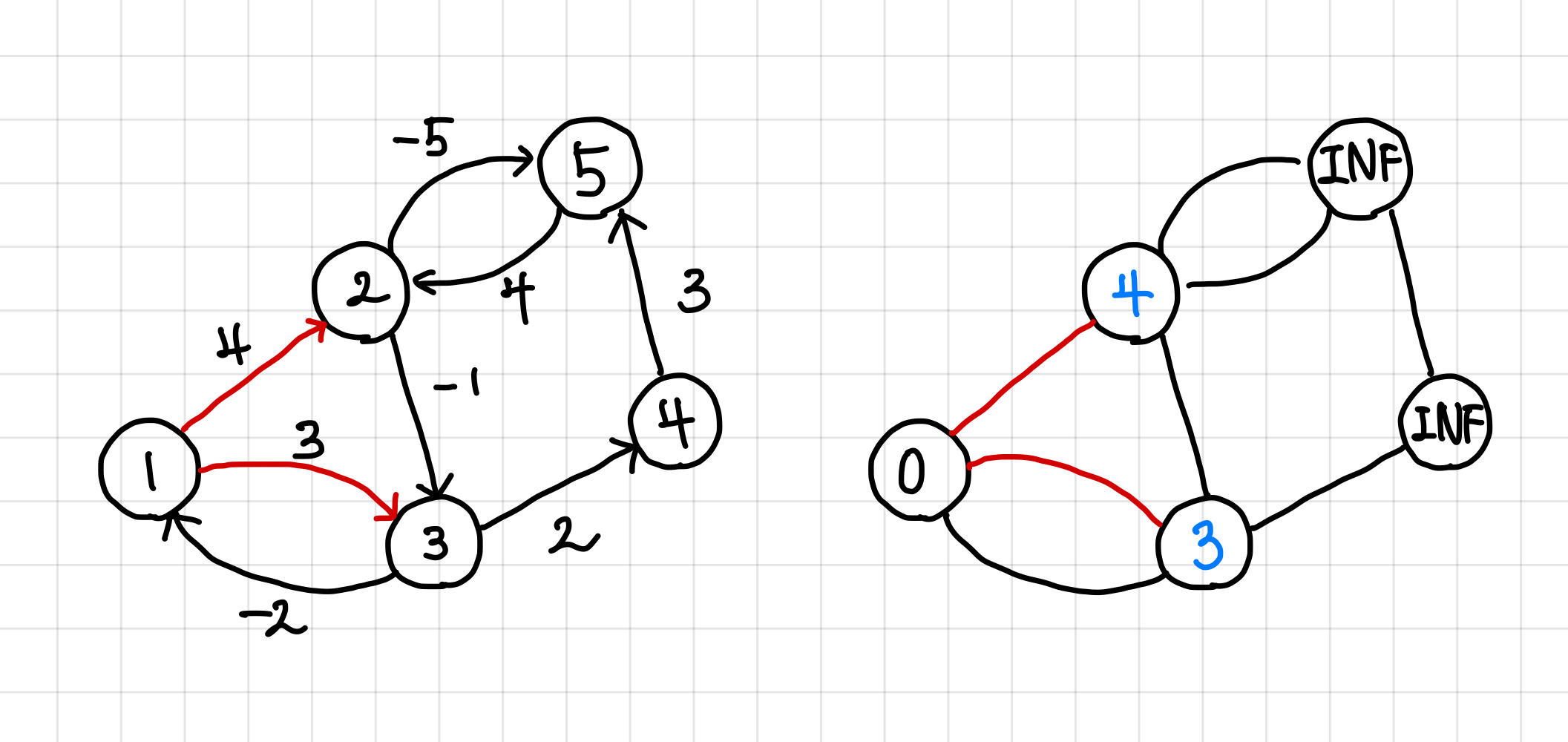
다음엔 2번에서 3번으로 가는 경우를 체크해보면, 4 - 1은 3이랑 같으므로 갱신하지 않는다.
마찬가지로 3번에서 1번으로 가는 경우, 3 - 2는 0보다 크므로 갱신하지 않는다. ▼
2번에서 5번 노드로 간다고 했을 때, 4 - 5 는 INF보다 작으므로 갱신해준다.
3번에서 4번 노드로 간다고 했을 때, 3 + 2 는 INF보다 작으므로 갱신해준다. ▼
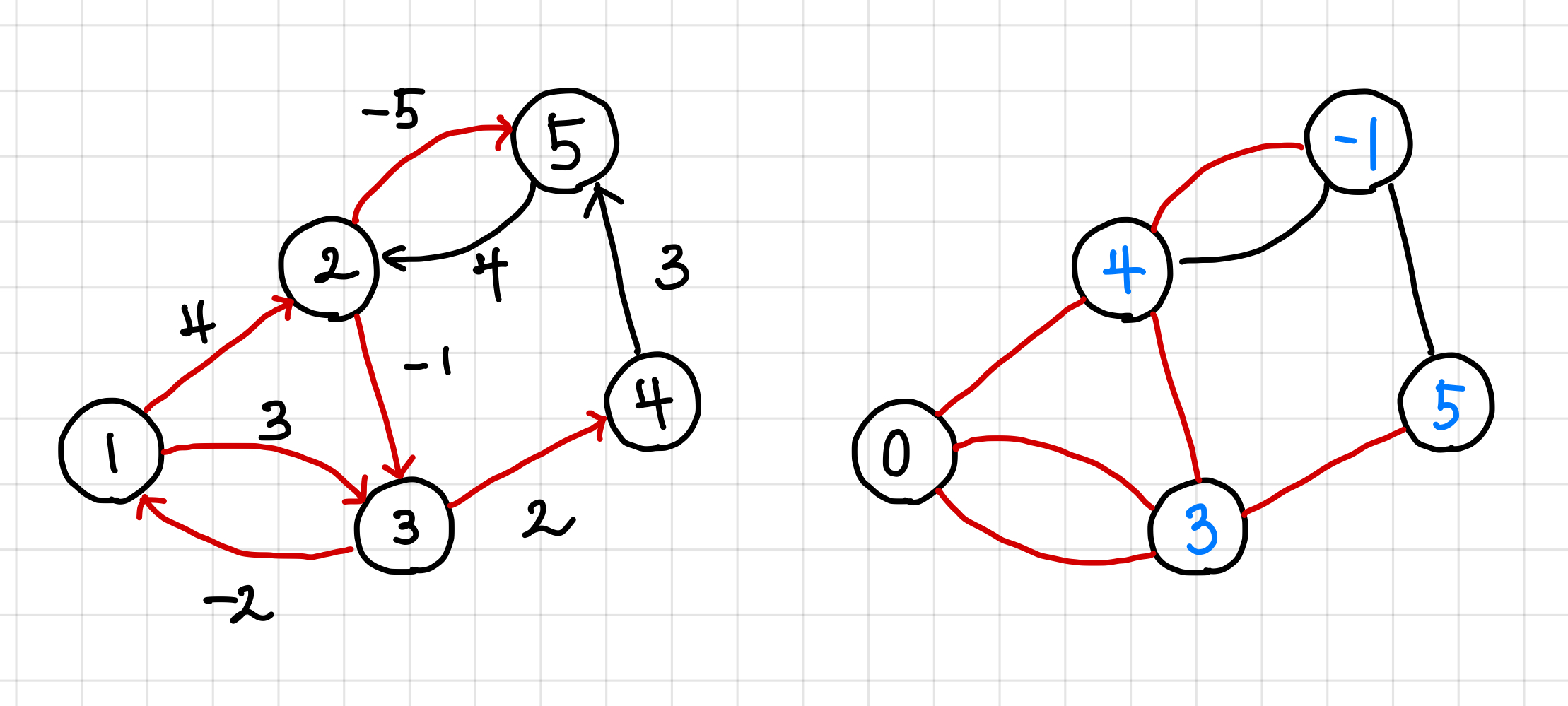
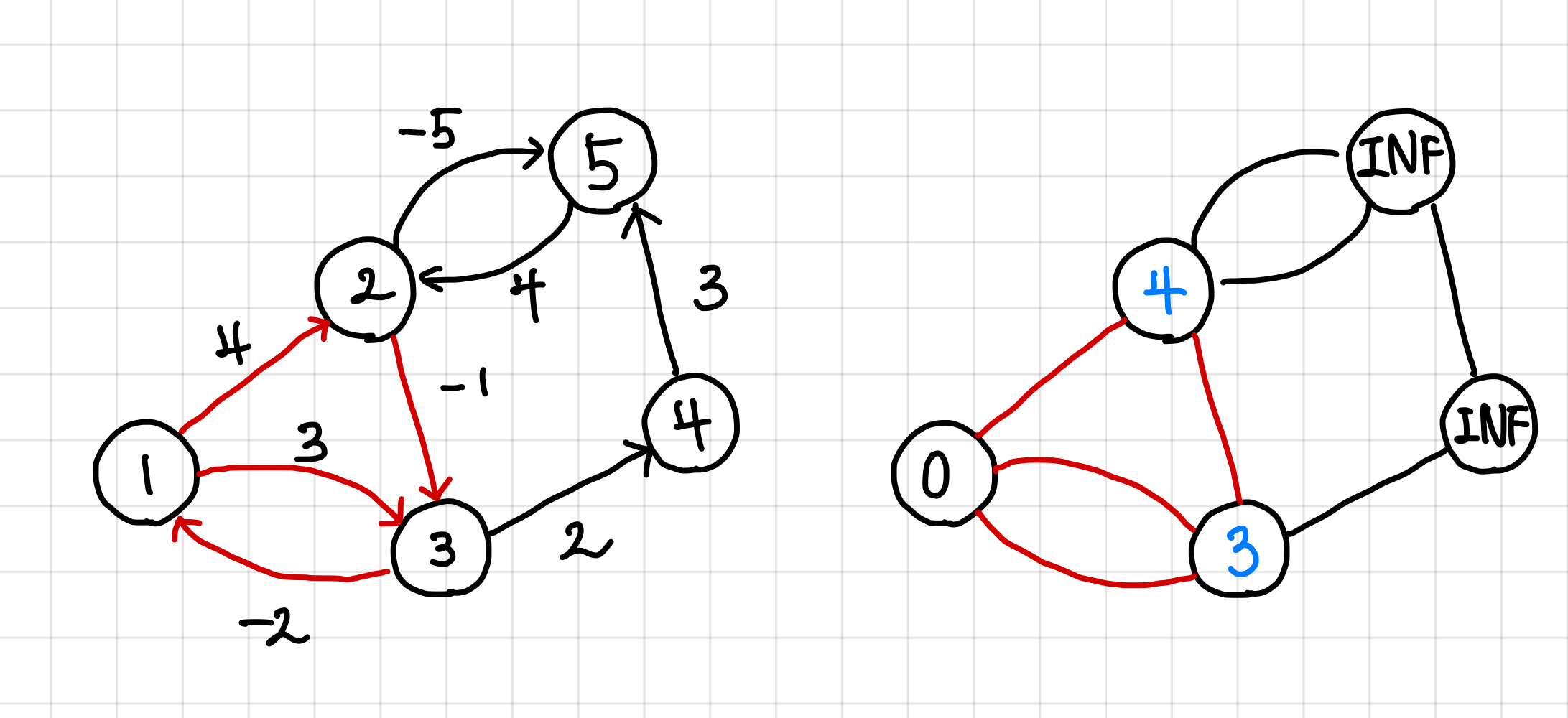
나머지 간선인 5번에서 2번과 4번에서 5번을 보면, 5번에서 2번 노드로 갈 시 값이 더 작아지므로 갱신해준다.
하지만 4번에서 5번으로 가는 경우는 -1이 5 + 3보다 더 작으므로 갱신해주지 않는다. ▼
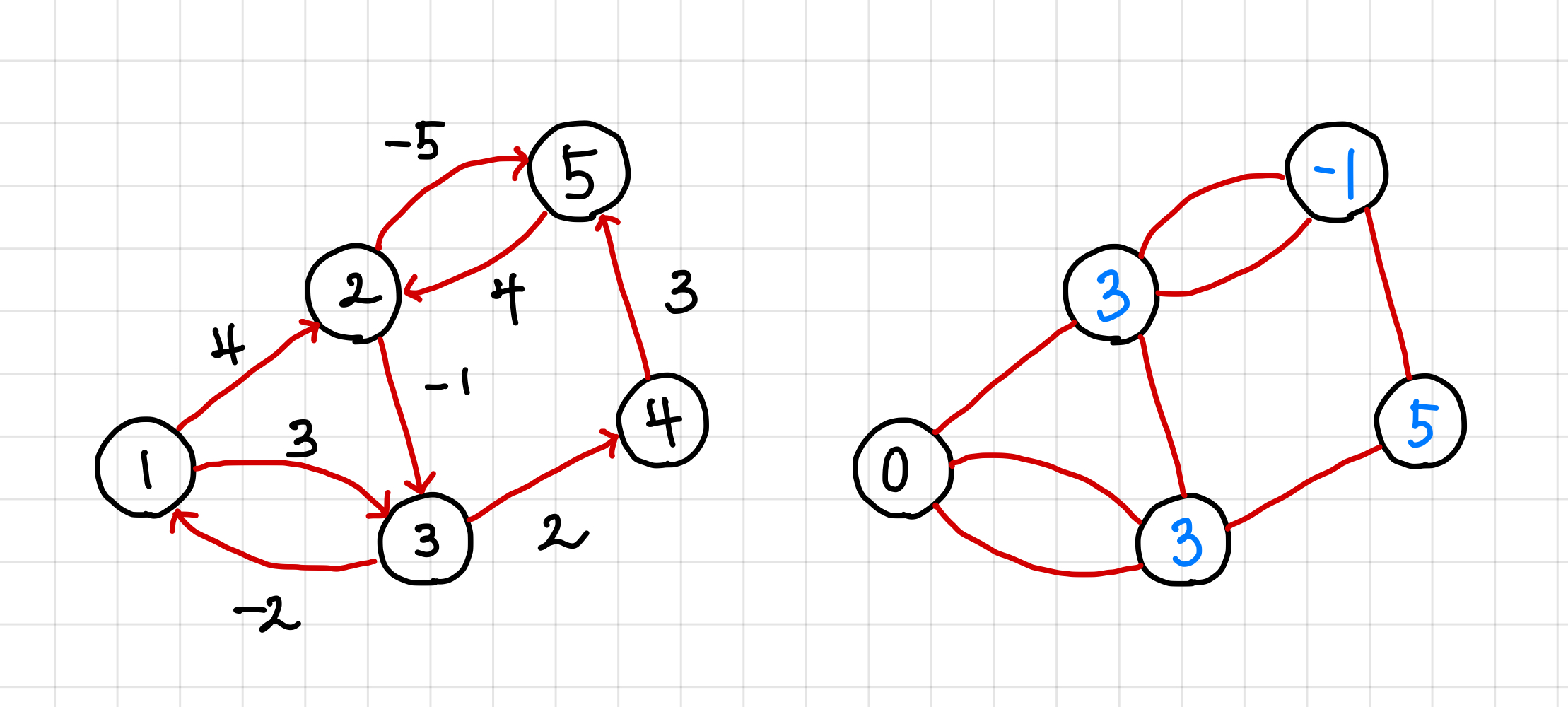
이렇게 모든 간선에 대한 순회가 1회 끝났다.
하지만 앞서 말한대로 음의 싸이클이 존재하는 경우 순회를 다시 한 번 더 돌리게 되면 값이 갱신되어 변하게 된다.
그리고 여러번 순회를 돌려주는 다른 이유는 간선 순회 순서에 따라 값이 갱신되지 않는 경우 다음 순회에서 그 값이 싸이클이 아니더라도 갱신되는 경우도 있기 때문이다.
일단 V - 1회를 돌려주기로 했으니, 같은 방식으로 나머지 3회를 마저 돌려보면 아래 처럼 변한다. ▼
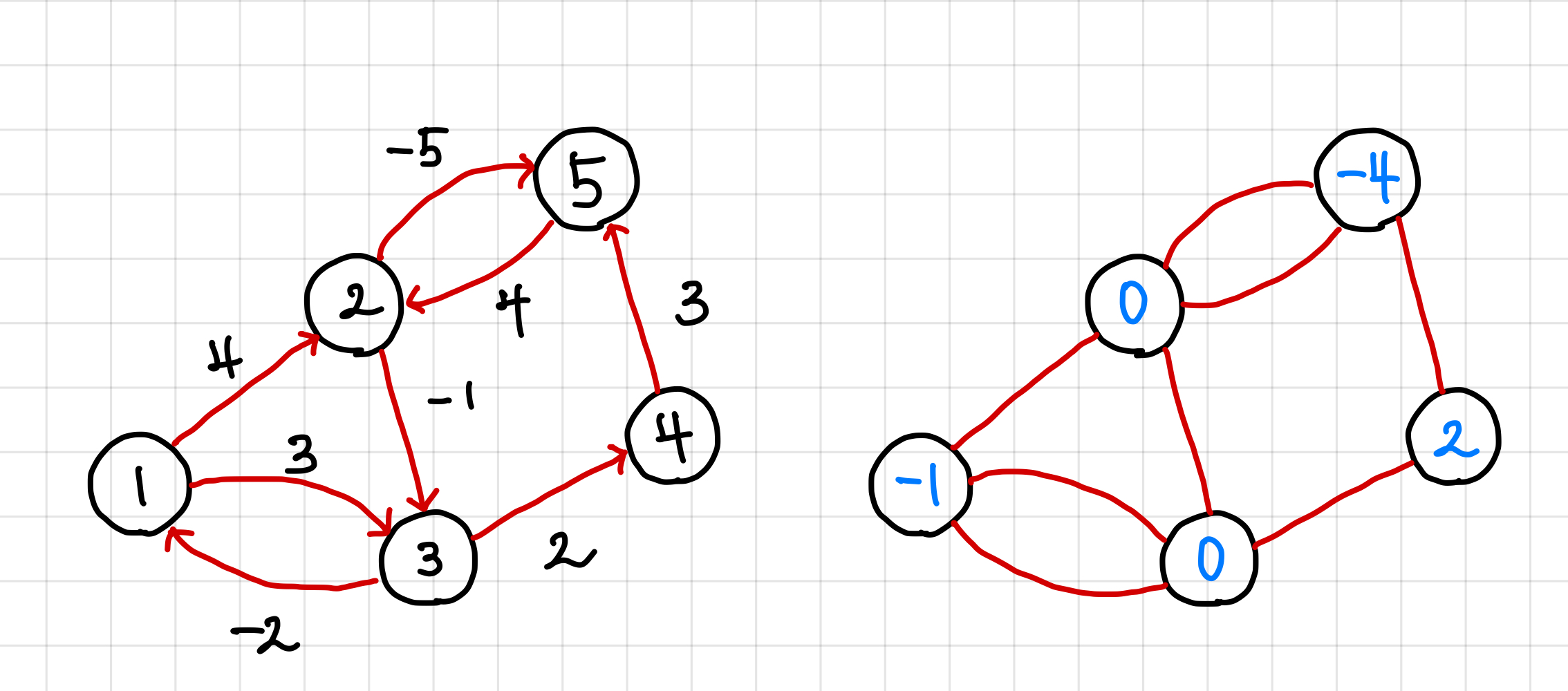
딱 보기에도 전체적으로 값이 다 줄었다.
보면 알겠지만 2번과 5번 사이에 음의 싸이클이 형성되어있기 때문에 값이 계속해서 줄어들어 다른 값들에도 영향을 준 것이다.
그럼 이제 음의 싸이클 판별을 해보자.
3. 순회를 한 번 더 돌려서 값이 변하는 지 체크해본다.
만약 한 간선이라도 값이 변하게 된다면, 그건 음의 싸이클이라는 증거다.
음의 싸이클이 없다면, 다른 값들의 갱신은 이루어지지 않는다.
위의 예시를 기준으로 순회를 돌면서 값이 바뀌는 부분을 체크해보면 세 군데가 바뀔 수있다고 나온다. ▼
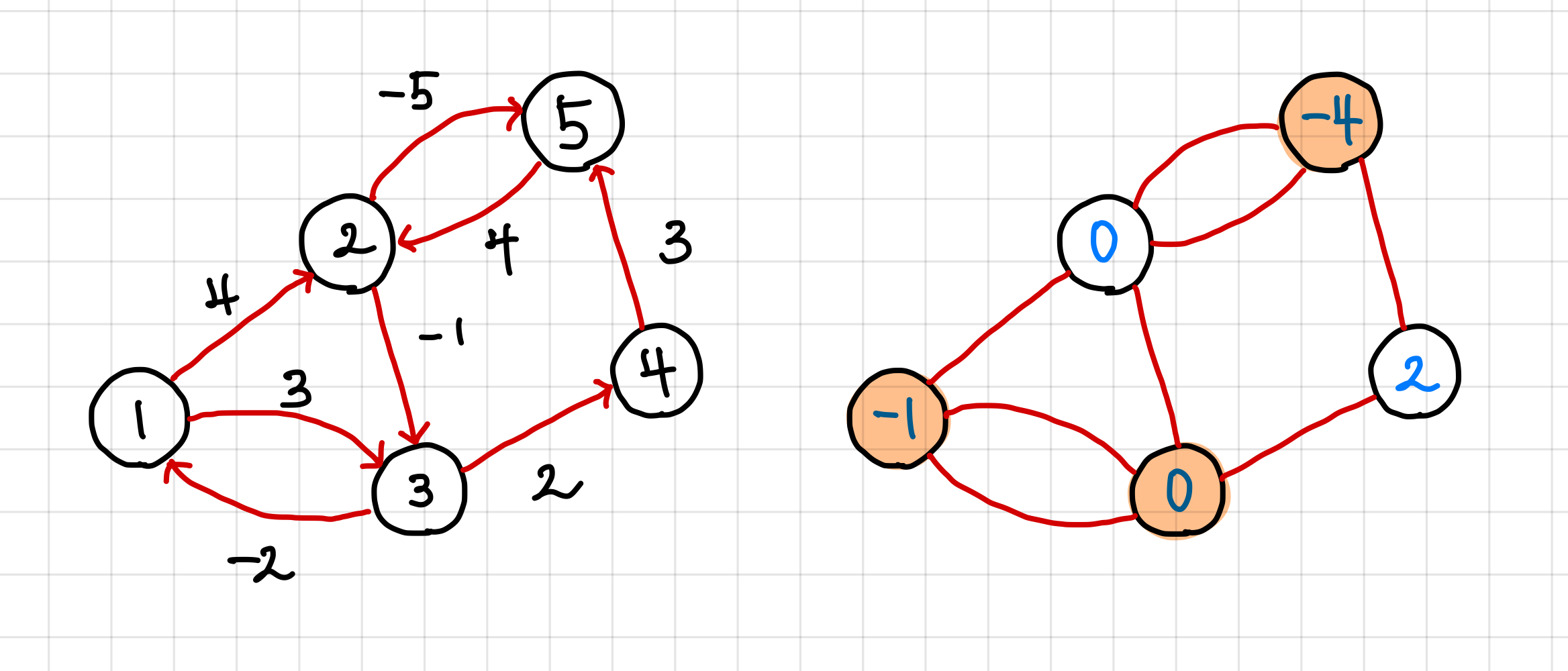
값이 갱신될 수 있으므로 이 그래프에서의 최단거리는 구할 수 없다.
하지만 만약 값이 갱신될 수 없다고 판별이 되면, V - 1번째 순회의 결과가 최단거리가 된다.
의사 코드
// 그래프의 자료구조 정의
record vertex {
list edges
real distance
vertex predecessor
}
record edge {
node source
node destination
real weight
}
// 벨만-포드 알고리즘
function BellmanFord(list vertices, list edges, vertex source)
// Step 1: 그래프 초기화
for each vertex v in vertices:
if v is source then v.distance = 0
else v.distance := infinity
v.predecessor := null
// Step 2: 이완 작업 반복
for i from 1 to size(vertices):
for each edge uv in edges:
u := uv.source
v := uv.destination // uv is the edge from u to v
if v.distance > u.distance + uv.weight
v.distance := u.distance + uv.weight
v.predecessor := u
// Step 3:
for each edge uv in edges:
u := uv.source
v := uv.destination
if v.distance > u.distance + uv.weight
error "Graph contains a negative-weight cycle"
시간복잡도
V와 E가 각각 그래프에서 꼭짓점과 변의 개수라고 한다면, 벨먼-포드 알고리즘의 실행시간은 O(|V| |E|)이다.
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 분리집합과 Union-Find (0) | 2024.02.17 |
|---|---|
| 플로이드 와샬 (0) | 2024.02.15 |
| 다익스트라 (0) | 2024.02.13 |
| MST, 최소 신장 트리 (0) | 2024.02.08 |
| 그래프와 그래프 탐색 (0) | 2024.02.07 |




