

개요
다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path)탐색 알고리즘이다.
특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다.
그러나 음의 간선을 포함할 수 없다.
음의 간선을 포함하려면 벨만-포드 알고리즘을 사용해야한다.
하지만 현실에는 음의 간선이 존재할 수 없기도 하고, 그게 아니어도 양의 간선만을 비교하는 상황에서도 다익스트라 알고리즘이 벨만-포드 알고리즘보다 빠르기 때문에 다익스트라 알고리즘을 선호하는 편이다.
알고리즘
알고리즘 분류와 특징
다익스트라 알고리즘이 다이나믹 프로그래밍 문제인 이유는 최단 거리가 단일 대상의 거리를 말하는 게 아니라 여러 개의 최단 거리의 합으로 이루어져 있기 때문이다.
거대한 최단 거리가 있다고 생각하면, 사실 그 내부는 자잘한 최단 거리들이 채워져 있다는 것이다.
기본적으로 다익스트라 알고리즘은 하나의 최단 거리를 구할 때, 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다.
즉, 메모이제이션도 활용을 한다는 것이다.
알고리즘 동작
그러면 본격적으로 알고리즘 동작 과정을 보자.
작동 과정은 이렇다
- 출발 노드를 설정한다.
- 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
- 저장된 최소 비용들 중 가장 적은 비용이 저장된 노드를 다음 노드로 설정한다.
- 다음 노드를 거쳐 특정 노드로 가는 경우가 생길 수 있으므로, 최소 비용을 갱신한다.
- 3번과 4번을 반복한다.
동작 예시
먼저 이런 식으로 그래프가 있다고 해보자. 그리고 1번 노드부터 시작한다고 하자.
그리고 각 노드 까지 가는 거리를 일단은 INF(무한)이라고 하자.
시작 노드의 거리는 0으로 둔다. ▼
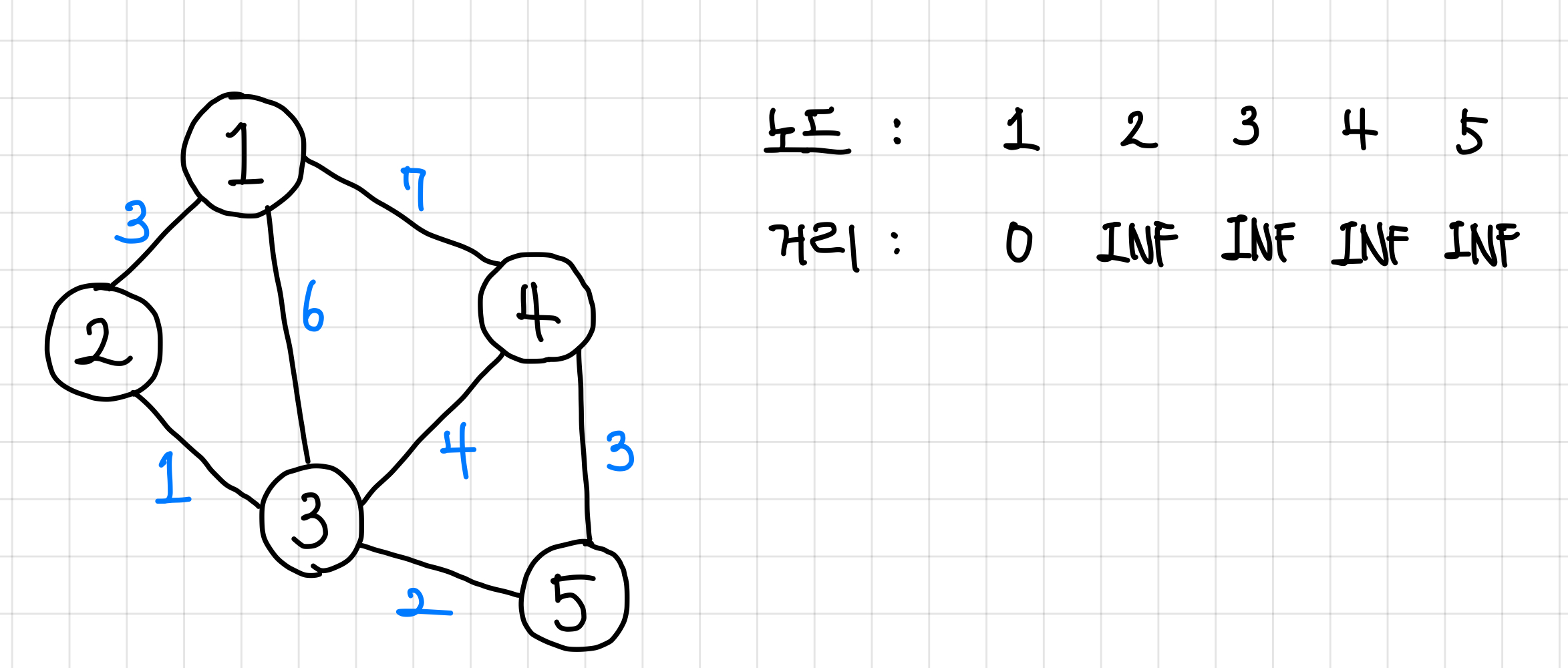
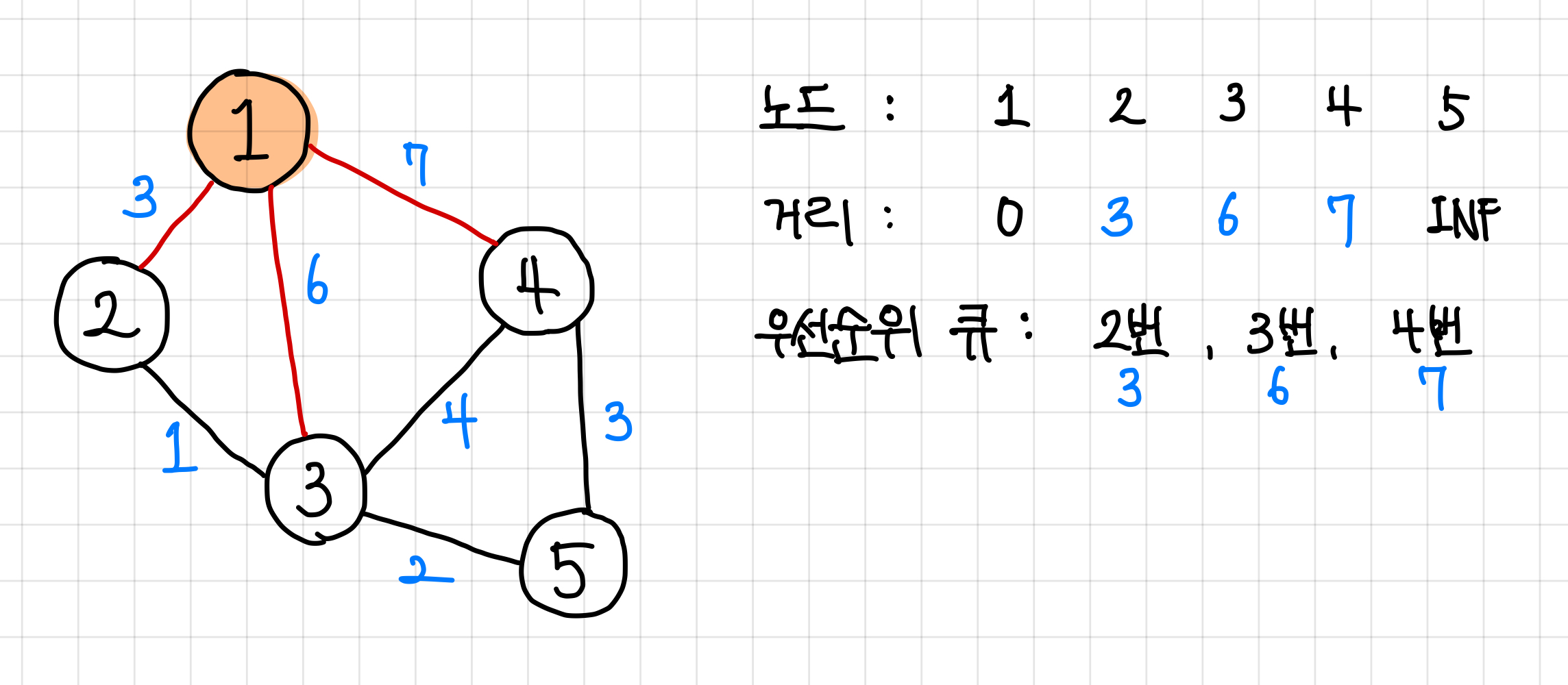
1. 일단은 1번 노드에 붙어 있는 노드인 2번, 3번, 4번 노드 까지의 최단 거리는 각각 3, 6, 7로 둘 수 있다.
그리고 이 값들은 현재 INF보다 당연히 작으므로 거리 값을 3, 6, 7로 바꿔준다.
확인한 노드 정보들을 우선 순위 큐에 넣어준다. ▼
간단한 우선 순위 큐 설명
우선 순위가 높은 값을 가장 앞에 배치하는 큐를 말한다.
우선 순위 큐를 사용한 이유는 가장 적은 비용이 저장된 노드를 다음 노드로 둬야하기 때문이다.
일반 큐를 사용한다면, 순서에 따라 들어가므로 가장 작은 값을 찾는 순회를 한 번 행해야하지만, 우선 순위 큐를 사용하면 맨 앞이 무조건 가장 작은 값이 된다.
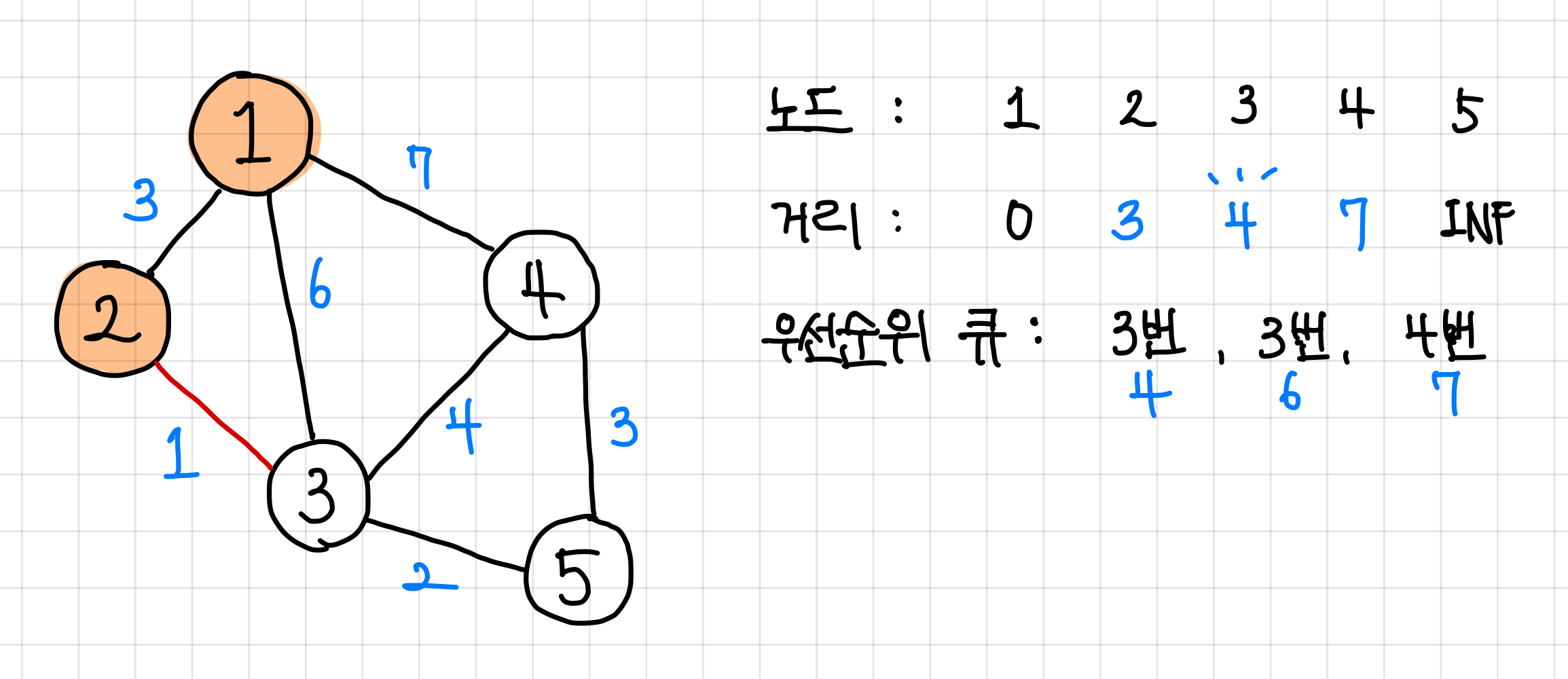
2. 우선 순위 큐에 들어간 값 중 가장 작은 값을 가진 노드는 2번 노드 이므로, 다음엔 2번 노드로 간다.
2번 노드에서 갈 수 있는 방향은 두 가지 이지만, 1번 노드는 이미 방문했으므로 3번 노드로 가는 값만 확인한다.
값을 확인해보니, 1번 -> 2번 -> 3번 값이 1번 -> 3번 값 보다 작으므로 값을 갱신해준다.
그리고 우선 순위 큐에 값을 넣어 준다. ▼
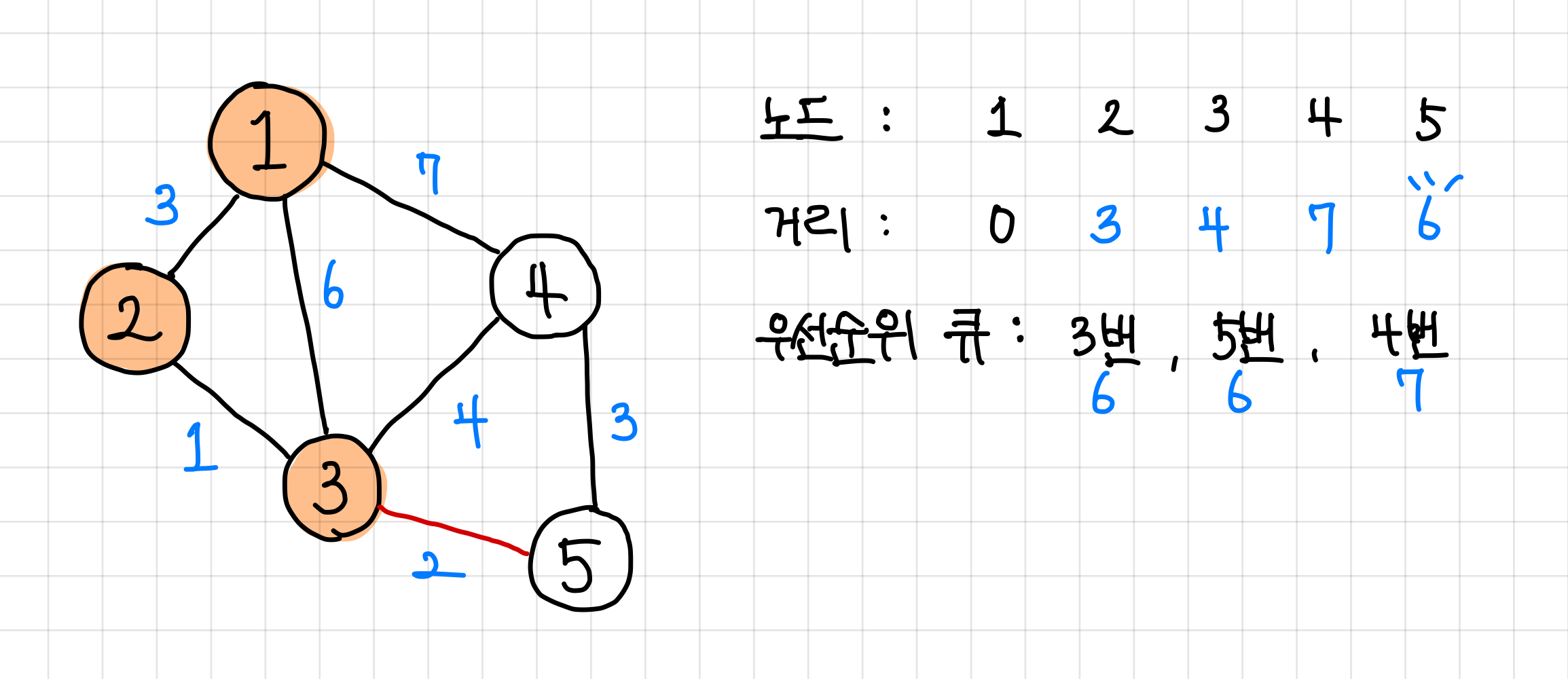
3. 우선 순위 큐에 들어간 값 중 가장 작은 값을 가진 노드는 3번 노드 중에서도 4 값으로 갱신된 3번 노드 이므로, 다음엔 3번 노드로 간다.
3번 노드에서 갈 수 있는 방향은 네 가지 이지만, 1번과 2번 노드는 이미 방문했으므로 4번과 5번 노드로 가는 값만 확인한다.
4번 노드로 갈 경우, 기존의 4번 노드에 있던 값보다 더 크게 되므로, 4번 노드의 값은 갱신하지 않고, 우선 순위 큐에도 넣지 않는다.
5번 노드로 갈 경우, 기존의 5번 노드 값이 INF였으므로, 값을 갱신해주고 우선 순위 큐에 넣어 준다.
6 값을 가진 3번 노드가 이미 있으므로, 3번 뒤에 들어간다. ▼
4. 다음에 갈 값은 6 값의 3번 노드이지만, 3번은 이미 방문해서 값이 갱신됐으므로 이 값은 버리고 다음 값인 5번 노드로 간다.
하지만 앞에서와 마찬가지로, 3번 노드는 이미 방문했고, 4번 노드로 가면 값이 기존 보다 더 커지므로 가지 않는다.
5번 노드에서는 갱신할 값이 없다.
그러므로 우선 순위 큐에 남아있는 4번 노드로 간다. ▼
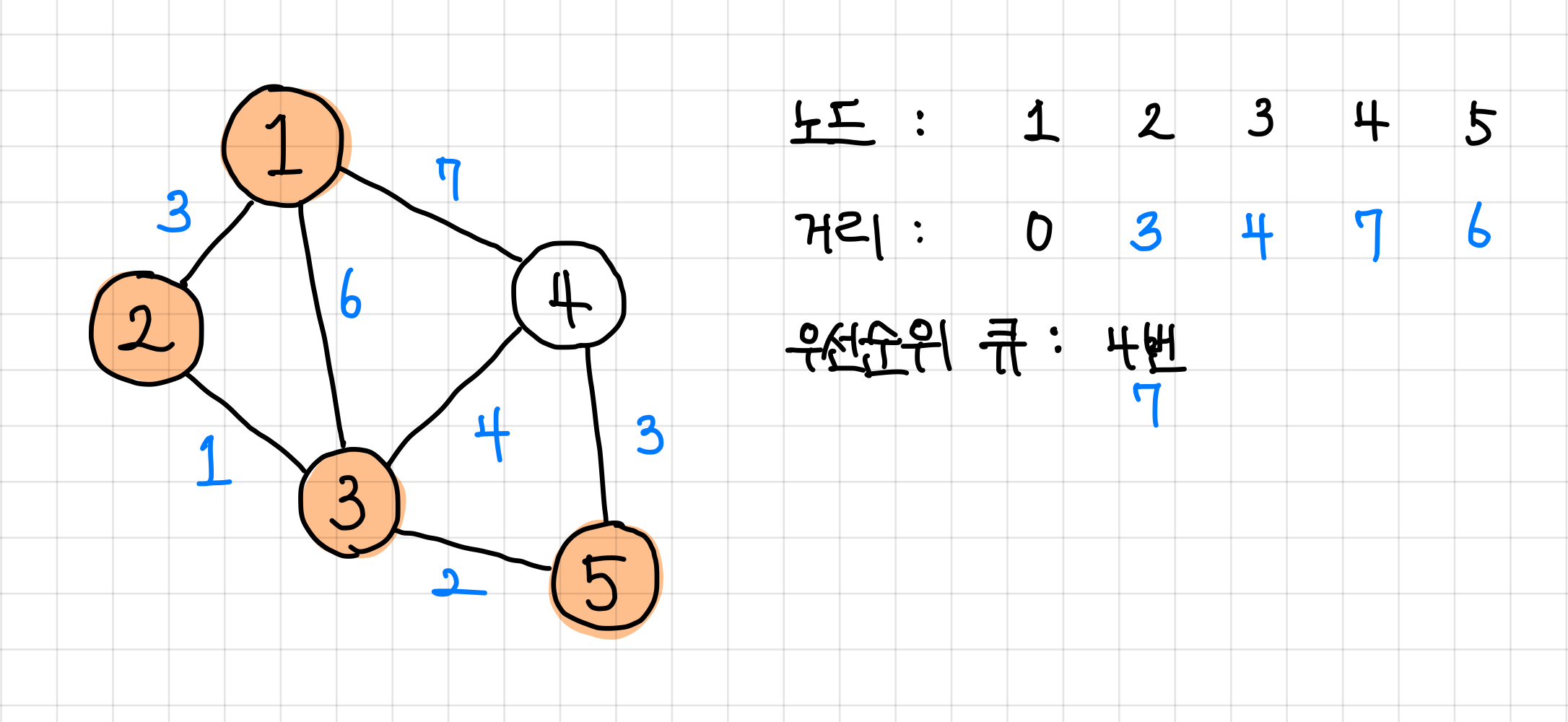
5. 4번 노드로 갈 때는 4번 노드를 통해서 다른 값으로 간 적이 없으므로, 방문한 노드는 1번 노드만으로 해놓고 다시 탐색해본다.
하지만 4번 노드를 통해서 가게 되면 기존의 값보다 더 커지므로, 아무 노드에도 방문하지 않는다.
방문할 노드가 더 이상 남아있지 않으므로 코드를 종료시킨다. ▼
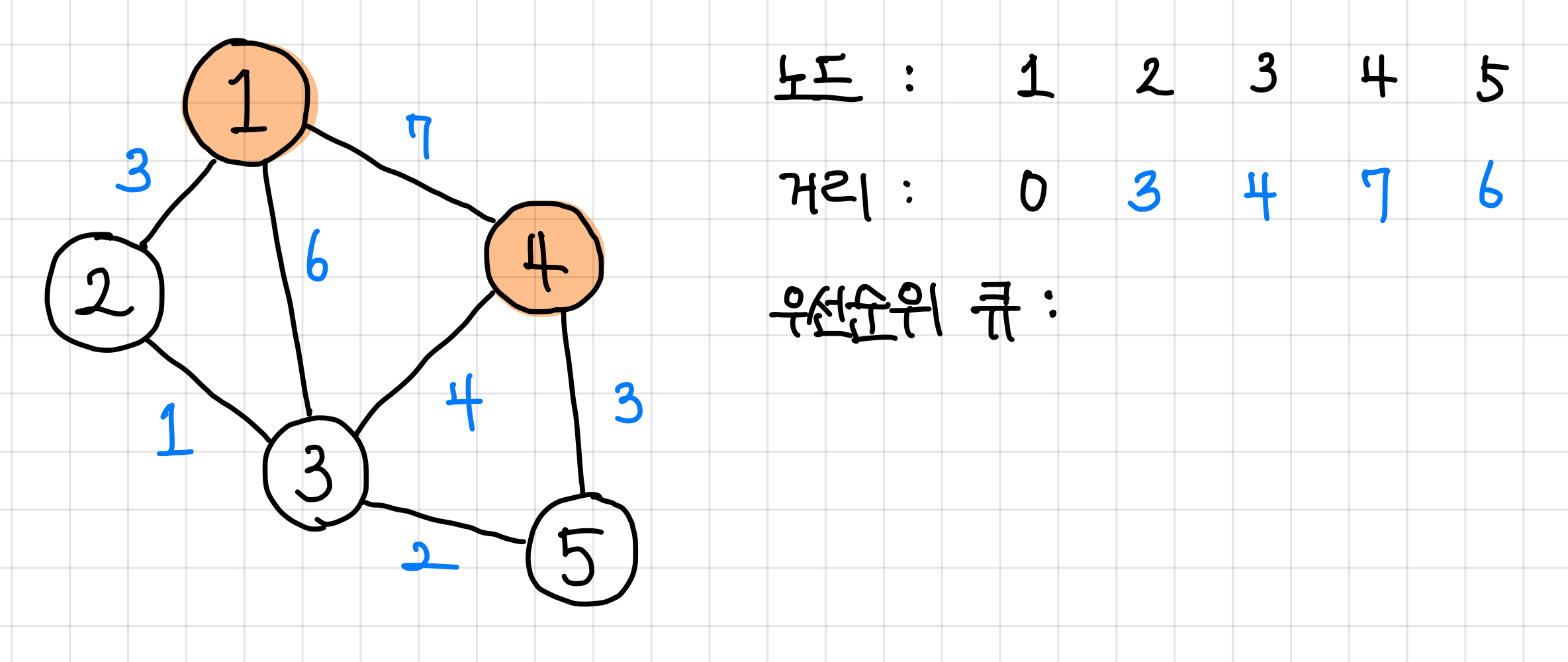
6. 코드를 종료했을 때 거리 값이 곧, 1번 노드에서 다른 노드로 가는 최단 경로가 된다. ▼

의사 코드
function Dijikstra(Graph, source):
dist[source] ← 0
create vertex set Q
for each vertex v in Graph:
if v ≠ source
dist[v] ← INFINITY
prev[v] ← UNDEFINED
Q.add_with_priority(v, dist[v])
while Q is not empty:
u ← Q.extract_min()
for each neighbor v of u:
alt ← dist[u] + length(u, v)
if alt < dist[v]
dist[v] ← alt
prev[v] ← u
Q.decrease_priority(v, alt)
return dist, prev
시간 복잡도
원래의 다익스트라 알고리즘은 우선순위 큐를 사용하지 않아서 시간 복잡도가 O(V^2) 이었다고 한다.
하지만 후에 우선순위 큐에 기반한 알고리즘이 만들어지면서 시간 복잡도가 O(E + VlogV)가 되었다.
(V는 꼭짓점의 개수이고, E는 변의 개수이다.)
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 플로이드 와샬 (0) | 2024.02.15 |
|---|---|
| 벨만 포드 (0) | 2024.02.15 |
| MST, 최소 신장 트리 (0) | 2024.02.08 |
| 그래프와 그래프 탐색 (0) | 2024.02.07 |
| 다이나믹 프로그래밍 (0) | 2024.02.07 |




