

개요
연결 리스트와 배열은 다른 자료구조를 구현할 때 기본이 되는 자료구조로 많이 사용이 되며 서로 비교되는 일이 많다.
스택, 큐, 덱과 같은 선형 자료구조들의 기본이 된다.
기초적인 단계의 자료구조들은 배열로 구현하기가 쉬워서 보통 배열로 많이 구현해보는데, 배열의 단점(후에 이야기 할 것이다.)으로 인해 이를 보완하고자 연결리스트를 사용하기도 한다.
둘 중 무엇을 사용하느냐는 자유지만, 둘의 특성을 잘 알아두고 상황에 맞게 응용하는 것이 가장 좋아보인다.▼
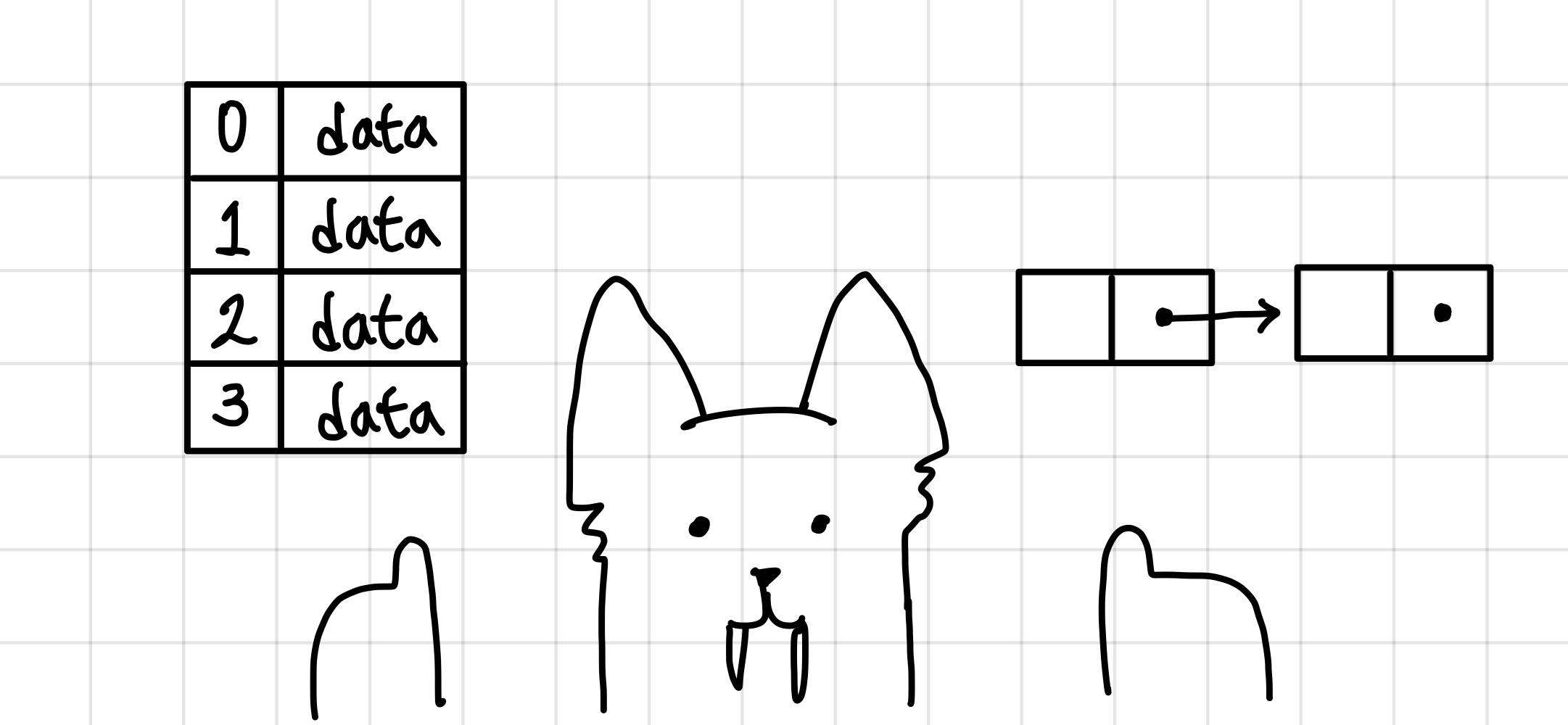
배열(array)
배열이란?
배열(array)은 연관된 데이터를 하나의 변수에 그룹화 하여 관리하는 자료구조이다.
말이 조금 어려울 수 있는데, 다들 알다시피 같은 데이터 타입 변수들을 모아놓은 것이다.
좀 더 세부적이고 명확하게 설명을 하자면, 동일한 크기의 메모리 공간이 빈틈없이 연속적으로 나열된 자료구조이다.
❓ 배열이 자료구조라고 하기엔 뭔가 빈약한데요?
배열의 경우에는 프로그래밍 언어에서 기본적으로 지원을 해서 하나의 변수로 볼 수도 있지만, 엄밀히 따지면 배열도 자료구조가 맞다.
애초에 자료구조들도 변수화 시킬 수 있긴 해서 변수가 된다고 자료구조가 아니란 것은 잘못된 이야기다.
배열의 구조와 장점
그러면 배열의 구조를 시각적으로 보자.
배열은 위에서 말한대로 동일한 크기의 메모리 공간이 빈틈없이 연속적으로 나열된 자료구조로서 메모리를 아래와 같은 형태로 차지하게 된다.▼

각 칸에는 메모리 주소로 접근이 되기 때문에 램의 Random Access가 가능하다.
array[n] = 10;
이렇게 바로 접근이 가능한 이유는 배열은 머리 부분 주소를 저장하고 있다가, 특정 인덱스에 접근할 때 머리 부분 주소 + 자료형 크기 * 인덱스 의 계산으로 접근하기 때문이다.▼

이런 특징 덕분에 배열은 굉장히 쉽고 간단하게 선언과 응용을 할 수 있다.
문제점
그러나 모든 것이 그렇듯, 배열에는 문제점이 존재한다.
크게 두 가지 문제가 있는데, 하나는 메모리 할당, 다른 하나는 추가와 확장이다.
메모리 할당 문제
앞에서 언급했듯이 배열은 `메모리가 빈틈없이 연속적으로 나열된 구조`다.
그런데 만약에 메모리 공간에 연속적으로 나열할 수 없는 상황이라면 어떨까?
이런 상황은 요즘과 같은 시대에서는 정말 말도 안되는 상황이다.
램 용량도 전에 비해 기하급수적으로 늘어나는 상황이고, OS 개발이 잘 되어있어서 램을 효율적으로 관리한다.
하지만 엄청나게 긴 배열을 선언할 때, 메모리가 아래와 같은 상황이라면 문제가 발생할 수 있다.▼

물론 어디까지나 이론적인 이야기고 우리가 일상적으로(?) 프로그래밍하면서 마주하기는 힘든 상황이다.
그래도 배열의 특성상 이러한 문제가 발생할 수 도 있다고 한다.
추가와 확장
일반적인 배열은 크기가 한 번 정해지고 나면 더 이상 크기를 바꿀 수 없다.
int 변수를 선언하고서 해당 변수를 long long 으로 바꿀 수 없는 것과 같이 일반적인 배열도 크기가 한 번 정해지고 나면 확장이나 축소가 불가능해진다.▼

C언어에서는 변수 값으로 배열을 선언하는 것도 불가능했기 때문에 배열 크기가 가변적인 상황에서는 굉장히 곤란했다.
int n = 10;
...
int array[n]; //C에서는 이런 문법은 없었다. C++은 가능하다.
그래서 C에서는 동적할당을 주로 사용했지만 이렇게 동적할당 한 배열도 크기를 조절하려면 다시 선언해줘야했다.
int n = 10;
int *array;
array = (int *)malloc(sizeof(int) * n);
...
array = realloc(array, sizeof(int) * (n + 10));
그런데 최근에 나온 신생 언어들을 보면 크기를 자유롭게 바꾸는 것을 볼 수 있다.▼

이 배열들은 도대체 뭘 어떻게 했길래 늘리고 줄이는게 자유로운걸까?
희소 배열(sparse table)
그 해답은 우리가 보는 일반적인 배열이 아니라서 이다.
모든 신생언어들의 배열이 같지는 않겠지만, 이 배열들은 배열 요소를 위한 메모리 공간이 꼭 동일한 크기를 갖지 않아도 된다.
심지어는 연속적으로 이어져있지 않을 수 도 있다.
이렇게 배열의 요소가 연속적으로 이어져 있지 않는 배열을 희소 배열이라고 한다.
희소 배열에 대한 설명은 다음에 추가적으로 진행하겠다.
일단은 희소 배열이란 것도 있다고 생각하면 된다.
장/단점 정리
앞에서 본 내용들을 보면 배열의 장/단점은 아래와 같이 정리할 수 있다.
장점
- 쉽게 선언하고 사용할 수 있다.
사용하기 굉장히 쉽고 간편하다는 것이 사용 이유의 절반 이상인 것 같다. - 각 인덱스에 접근하는 시간이 굉장히 빠르다.
Random Access.
단점
- 연속된 메모리가 없다면 선언할 수 없다.
하지만 이런 일은 요즘 메모리에서는 쉽게 발생하지는 않는다.
프로그램이 무거워지면 발생할 수 도 있다. - 크기를 자유롭게 변경하기가 힘들다.
희소 배열로 구현되어있다면 쉽게 크기 조절을 할 수 있다.
하지만 희소 배열은 이름만 배열이지, 일반적인 배열의 형태는 아니다.
연결 리스트(linked list)
연결 리스트란?
연결 리스트는 각 노드가 데이터와 포인터를 가지고 연결되어있는 자료구조를 말한다.
이름에서도 보이듯이 노드들이 연결되어있는 구조로, 노드 내부에 있는 포인터가 다음 또는 이전 노드와 연결을 한다.
연결 리스트의 구조와 장점
연결 리스트의 구조를 시각적으로 보자.
연결 리스트는 노드들이 연결되어 있는 구조이다.
그림으로 보면 아래와 같다.▼

노드란?
노드는 데이터와 연결점을 갖고 있는 하나의 자료형이다.
연결 리스트의 기본 단위라고 할 수 있다.
일반적으로 데이터 변수와 다음 노드를 가리키는 포인터로 구성되어있다.
"딱 보기에도 불편해보이는데 왜 연결리스트를 사용하는거죠?"
연결 리스트를 사용하는 이유는 연결리스트가 메모리에 할당되는 방식 때문이다.
연결 리스트의 각 노드들은 연속적으로 배정되지 않는다.
우연하게 연속적으로 배정될 수도 있기는 하나, 일반적으로는 연속적으로 배정되지 않는다.
메모리 공간에 랜덤하게 배치되고, 이들이 서로 연결되는 방식이다.▼

이 방식의 장점은 배열의 문제를 보완해준다.
이전의 배열은 연속된 공간이 존재하지 않으면 할당할 수 없던 것에 비해, 연결리스트는 어쨌든 할당하려는 공간이 존재하기만 하면 할당이 가능해진다.▼

두 번째로는 확장과 축소가 자유롭다는 것이다.
포인터로 연결되어있고, 각 노드는 하나의 변수이기 때문에 새로운 변수를 할당하거나 할당된 변수를 할당 해제하는 방식으로 연결리스트를 확장, 축소 할 수 있다.▼

문제점
배열의 문제점을 완벽히 보완한 것 같지만, 배열에선 당연히 되는 것들이 안되는 문제점이 생겼다.
바로 Random Access가 안된다는 것이다.
배열에서는 주소 계산으로 내가 원하는 인덱스에 바로 접근이 가능했다.
배열에는 주소에 대한 일정한 규칙이 있었지만, 연결 리스트에는 주소에 대한 일정한 규칙이 없다.
그렇기에 주소 계산으로 다음 인덱스가 어디있는지 알 수 없고, 무조건 노드에 저장되어있는 다음 주소 정보를 확인해야 다음 인덱스가 어디있는지 알 수 있다.
무조건 노드를 열어봐야 알 수 있다는 것이다.▼

Random Access가 안되면 특정 인덱스에 접근하기까지 시간이 많이 걸린다.
세 번째에 접근하고 싶다면 앞의 첫 번째와 두 번째의 인덱스에 먼저 접근해야하고,
열 번째에 접근하고 싶다면 앞의 첫 번째 부터 아홉 번째의 인덱스 까지 접근해야 한다.
N번째 인덱스에 접근하려면, 인덱스에 접근하는 연산을 N번 해야한다는 것이다.▼

이렇게 되면 메모리 효율성은 증가하지만 접근하는데 시간이 오래걸리게 된다.
심지어는 3번째에 접근했다가, 2번째에에 접근할 일이 생기면 뒤로 돌아가는 포인터가 없어서 다시 처음부터 접근해야할 수 도 있다.
장/단점 정리
위의 설명들을 토대로 연결 리스트의 장/단점을 아래와 같이 요약할 수 있다.
장점
- 메모리 효율성이 좋다.
연속된 메모리를 할당하지 않아도 된다. - 추가와 확장이 자유롭다.
메모리 삭제와 추가가 쉽다.
단점
- 메모리 접근이 느리다.
Random Access가 안된다.
N번째 메모리에 접근하려면 0번째 부터 하나씩 접근해야한다.
마치며
배열과 연결 리스트는 후에 볼 자료구조들의 주춧돌이 되는 자료구조들이라 굉장히 중요하다.
선형구조들은 배열과 연결 리스트로 구현을 많이 하며, 비선형구조들도 선형 구조에서 따온 것들이 꽤 있어서 이해가 쉬워진다.
글에 다 담지 못한 것들이 많아서 아쉽지만, 일단은 이정도만 보고 다음에 더 보는 것으로 하자.
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 트리(tree) (0) | 2024.01.27 |
|---|---|
| 기본적인 자료구조 (0) | 2024.01.27 |
| 정렬 - 거품 정렬부터 셀 정렬까지 (0) | 2024.01.22 |
| 브루트 포스 (0) | 2024.01.20 |
| 간단한 수학(+ 약간의 정수론) (0) | 2024.01.19 |




