

개론
기하와 벡터, 행렬 식과 같은 수학이 아닌 중학생때 배웠던 기초적인 수학에 관한 알고리즘에 대한 설명이다.
정수론의 내용도 포함되어있다.
(몇가지는 중학생때 제목만 들었던 거고 자세하게 배우지 않았던 것일 수도 있다.)
나머지 연산
모듈러 연산이라고도 하고 나머지 연산에 관한 다른 공식들이나 정리들은 이산수학에서 배울 수 있다.
더 자세한 것은 이산수학에서 모듈러 연산에 대해서 보기로 하고 이 글에서는 나머지 연산에 대한 간단하고 응용하기 좋은 공식 몇가지를 볼 것이다.
나머지 연산의 경우 답이 매우 커질 때, 어떤 수로 나눈 나머지를 답으로 요구하기도 한다. 그 외에도 원 순환을 구현할 때도 사용한다.
나머지 연산은 우리가 따로 나누고, 빼고 할 필요 없이 나머지 연산자라는 것이 있어 바로 구하는 건 쉽다.
허나 값이 너무 큰 값에 대해 나머지 연산을 할 때는 값을 나눠서 나머지 연산을 해줘야 한다.
아래는 오버플로우가 나지 않게끔 나머지 연산을 해주는 방법이다.
- (a + b) % M = ((a % M) + (b % M)) % M
- (a * b) % M = ((a % M) * (b % M)) % M
- (a - b) % M = ((a % M) - (b % M) + M) % M
최대공약수(GCD)와 최소공배수(LCM)
최대공약수(Great Common Divisor)
정수 A와 B의 공통된 약수 중에서 가장 큰 정수.
구하는 방법 중 가장 간단하면서 직관적인 방법은 2부터 min(A, B)까지 나눠보는 것이다.
하지만 min(A, B)가 엄청나게 큰 수라면 시간이 굉장히 오래걸리게 된다.
그래서 더 빠르게 구하는 방법이 유클리드 호제법을 이용한 방법이다.
유클리드 호제법:
a % b = r 일 때, GCD(a, b) = GCD(b, r)
위의 공식을 이용해서 반복계산을 하다가, r이 0일 때 b값이 최대공약수가 된다.
반복 계산을 할 때 보통 재귀를 사용한다. (그렇다고 무조건 재귀를 써야하는 건 아니다.)
예제 코드
int GCD(int a, int b) {
int r = a % b;
if (r == 0)
return b;
else
return GCD(b, r);
}
최소공배수(Least Common Multiple)
정수 A와 B의 공통된 배수 중에서 가장 작은 정수.
LCM = A * B / GCD(A, B)
최대공약수를 구하면 최소공배수는 바로 구할 수 있다.
소수
한 소수에 대한 판별 : a * b
가장 쉬운 방법은 2부터 자기 자신 전까지 한 번씩 다 나눠보는 것이다.
그런데 조금만 생각해봐도 이 방법은 시간이 오래걸림을 알 수 있다.
"그런데 만약 10억 넘는 수가 들어온다면?"
운이 좋아서 그 수가 소수가 아니면 금방 끝나서 다행이지만, 그 수가 소수라면 10억번 연산하게 된다.
"그렇다면 어떻게 해야할까?"
일단 그에 대한 해답은
해당 수의 제곱근 값까지만 연산하면 된다는 것이다.
일단 어떠한 수는 a * b로 표현할 수 있다.
일단 a는 b보다 작다고 하자.
소수의 경우에는 1 * 자기자신 으로 나타내지겠지만, 소수가 아니라면 a가 1이 아닐 것이다.
그렇다면 a * b 를 잘 보자.
a를 1부터 시작해서 조금씩 키워나가보자.
그러면 어느 순간부터는 b보다 커지게 된다.
그때부터는 a * b의 위치가 뒤바뀌는 시점이면서, 더 이상 계산할 필요가 없는 부분이 된다.
커진 a가 지금까지 계산했던 b가 될 것이기 때문이다.
예를 들어보자,
24라는 수를 나누어 떨어지는 값 a, b로 표현을 해보겠다.
- 1 * 24 = 24
- 2 * 12 = 24
- 3 * 8 = 24
- 4 * 6 = 24
- 6 * 4 = 24
- 8 * 3 = 24
- 12 * 2 = 24
- 24 * 1 = 24
4번과 5번 사이의 인덱스를 중심으로 좌우 대칭된 걸 볼 수 있다.
이 말은 어떤 수 n의 제곱근 값까지만으로도 나눠도 약수를 다 구할 수 있다는 것이다.
즉, n의 제곱근 값 전에 (1제외) 나누어 떨어지는 값이 있다면 소수가 아닌것이다.
그래서 121이 들어오면 121을 다 계산하는게 아니라 11까지만 계산해보면 된다.
에라토스테네스의 체
앞의 소수 판별은 수 하나를 대상으로 한 것이라면, 에라토스테네스의 체는 범위 내의 소수를 모두 구하는 방법이다.
에라토스테네스의 체의 소수 판정 과정은 아래와 같다.
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. ▼

2. 2는 소수 이므로 2를 써준다. ▼
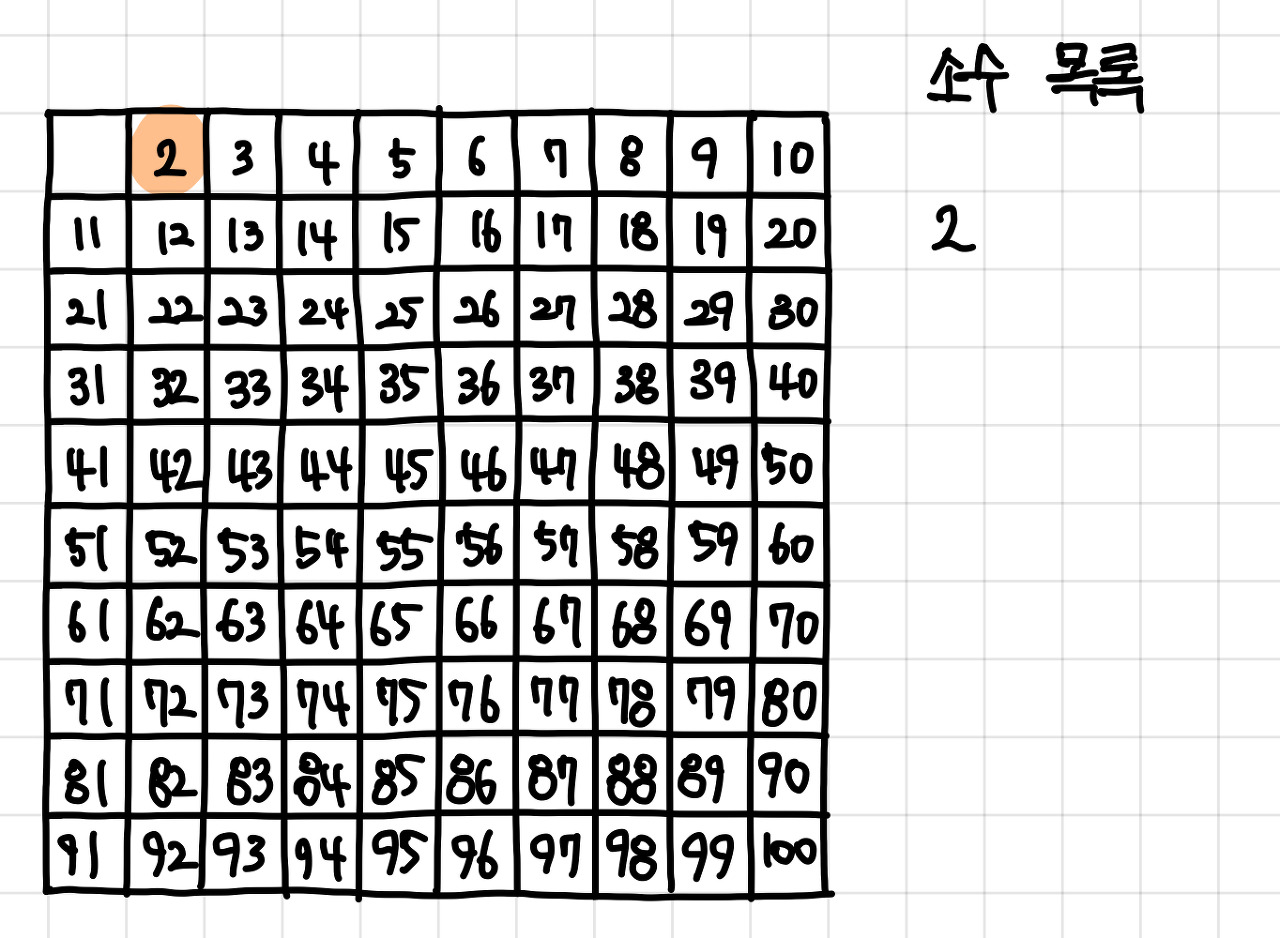
3. 자기 자신을 제외한 2의 배수를 모두 지운다. ▼
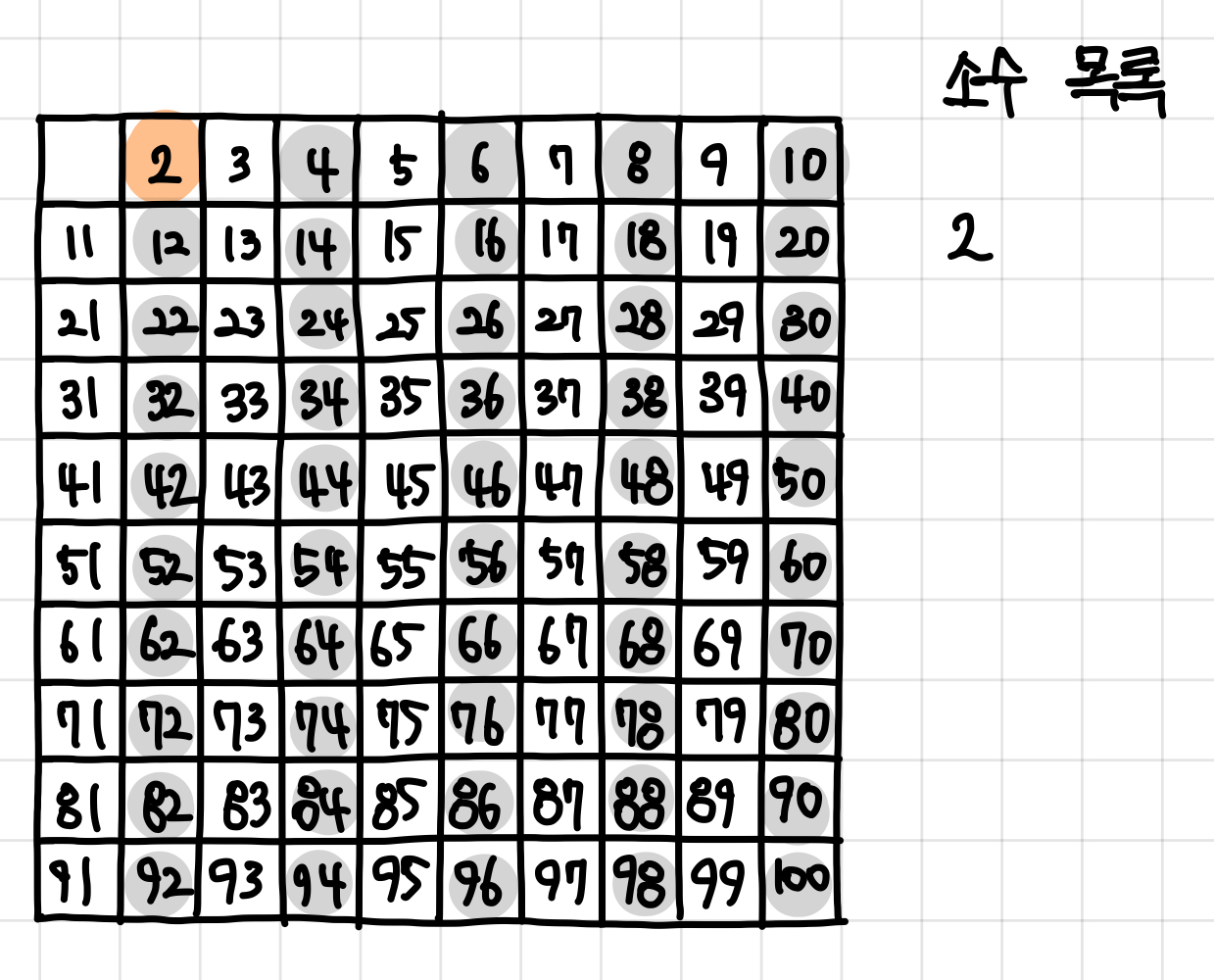
4. 남아 있는 수 가운데 3은 소수이므로 3을 써준다. ▼
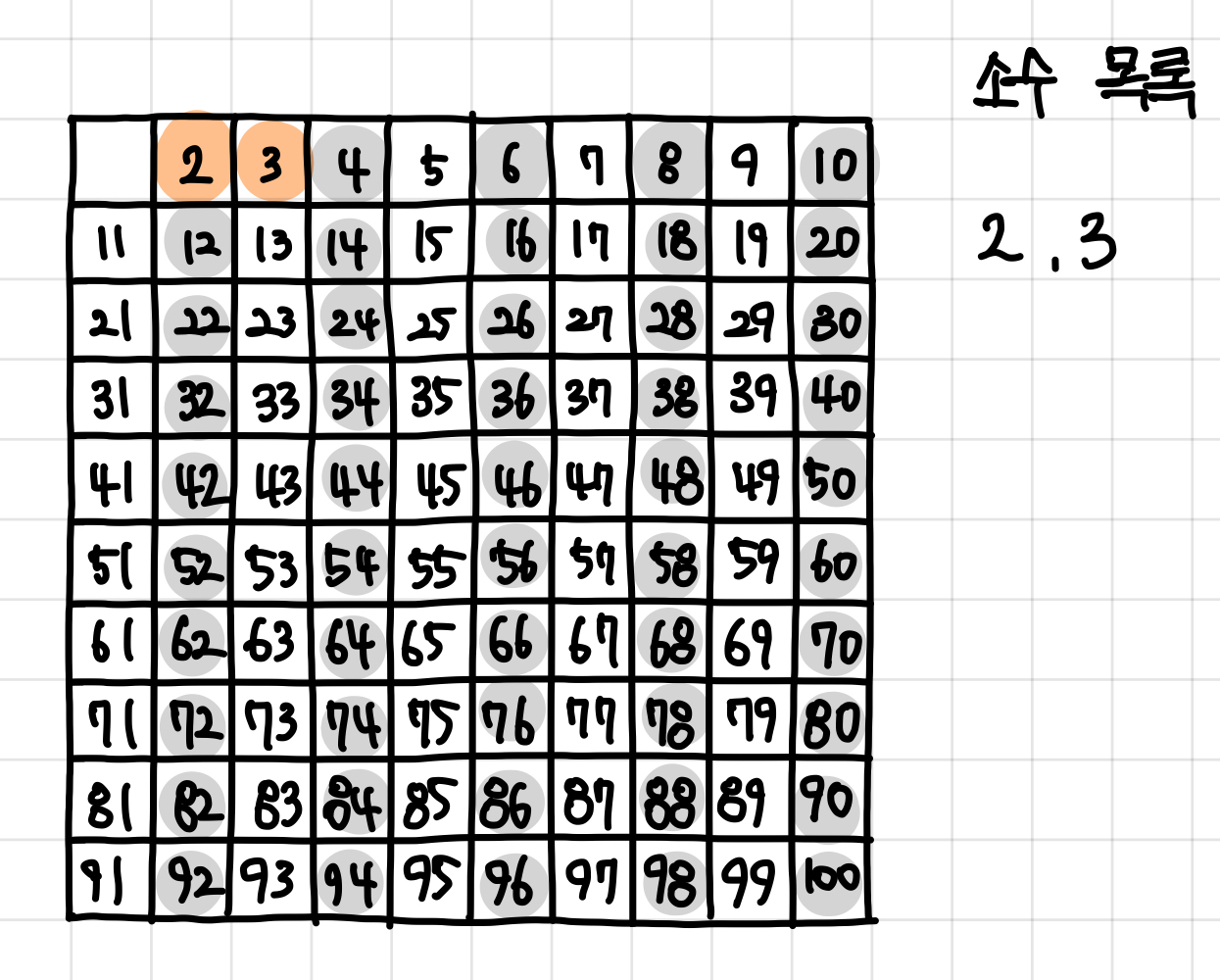
5. 자기 자신을 제외한 3의 배수를 모두 지운다. ▼
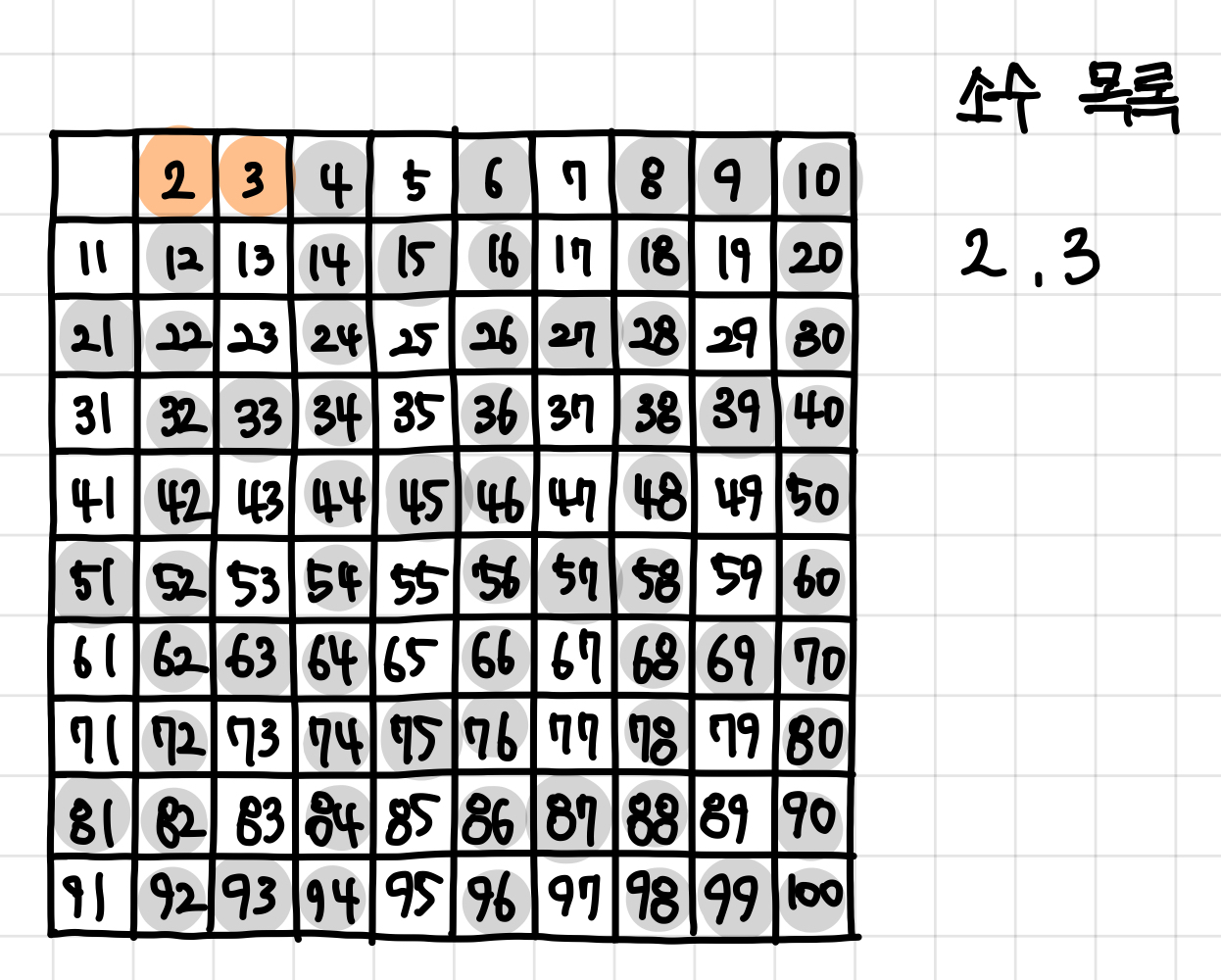
6. 남아 있는 수 가운데 5는 소수이므로 5를 써준다. ▼
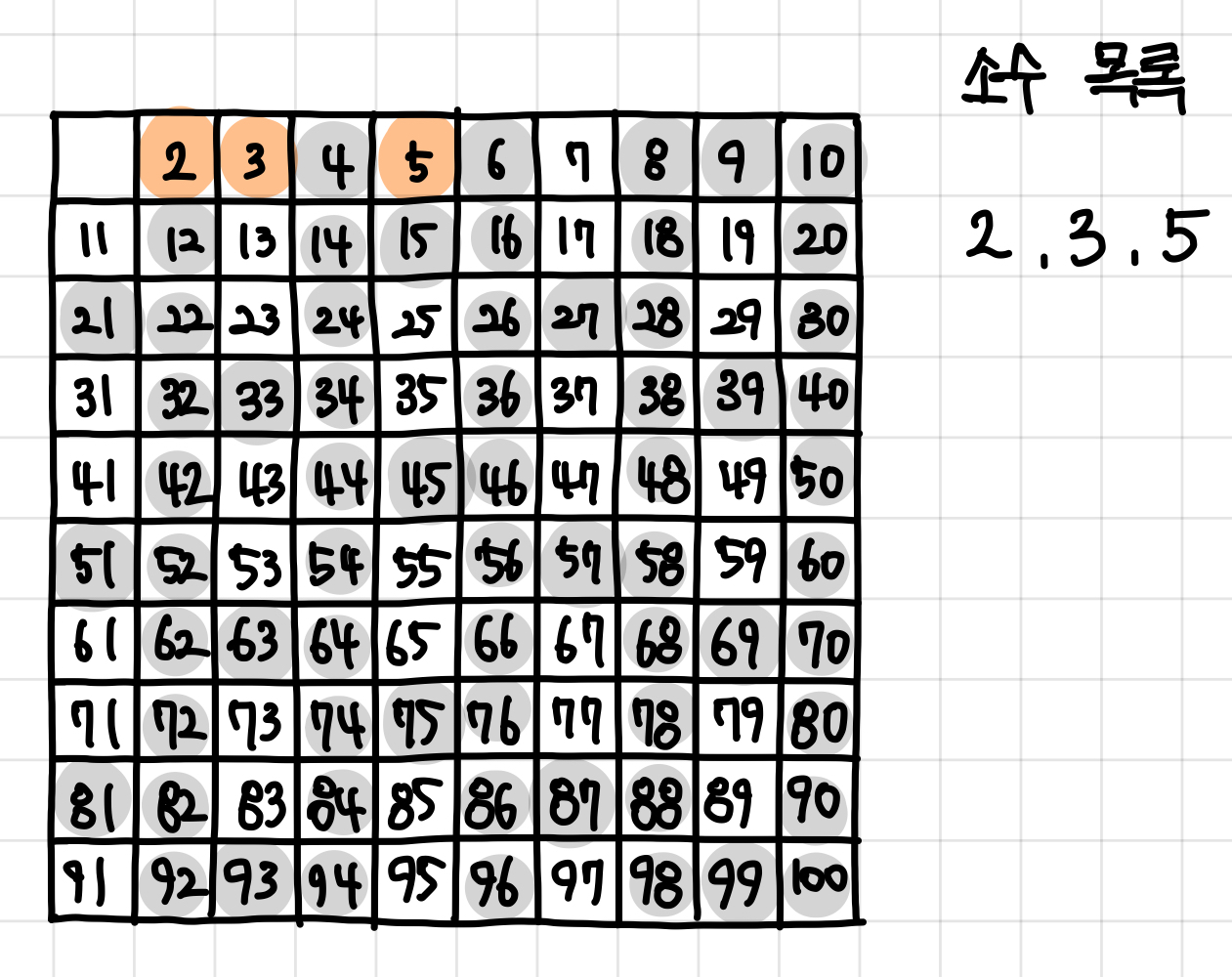
7. 자기 자신을 제외한 5의 배수를 모두 지운다. ▼
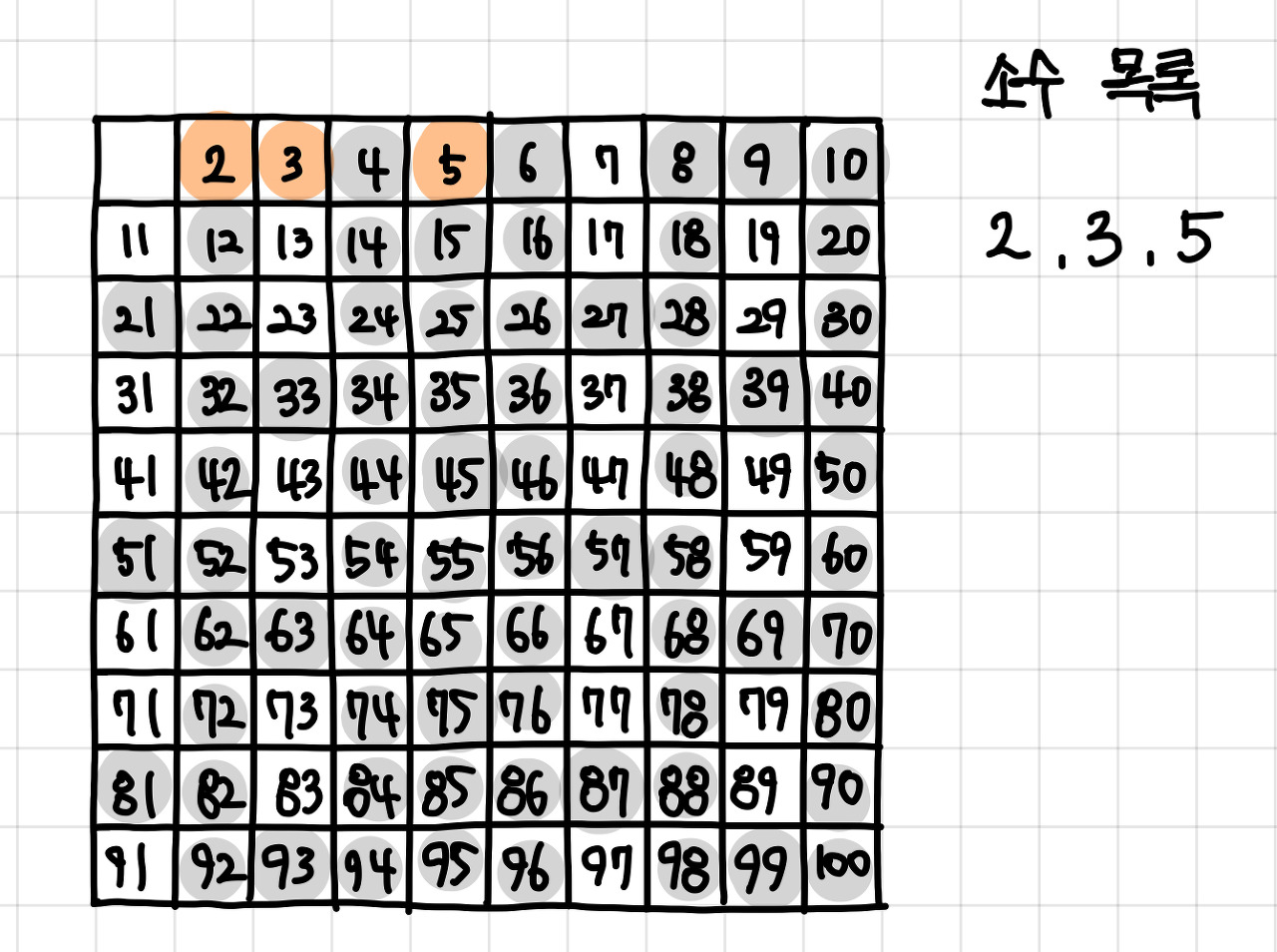
8. 남아 있는 수 가운데 7은 소수이므로 7을 써준다. ▼
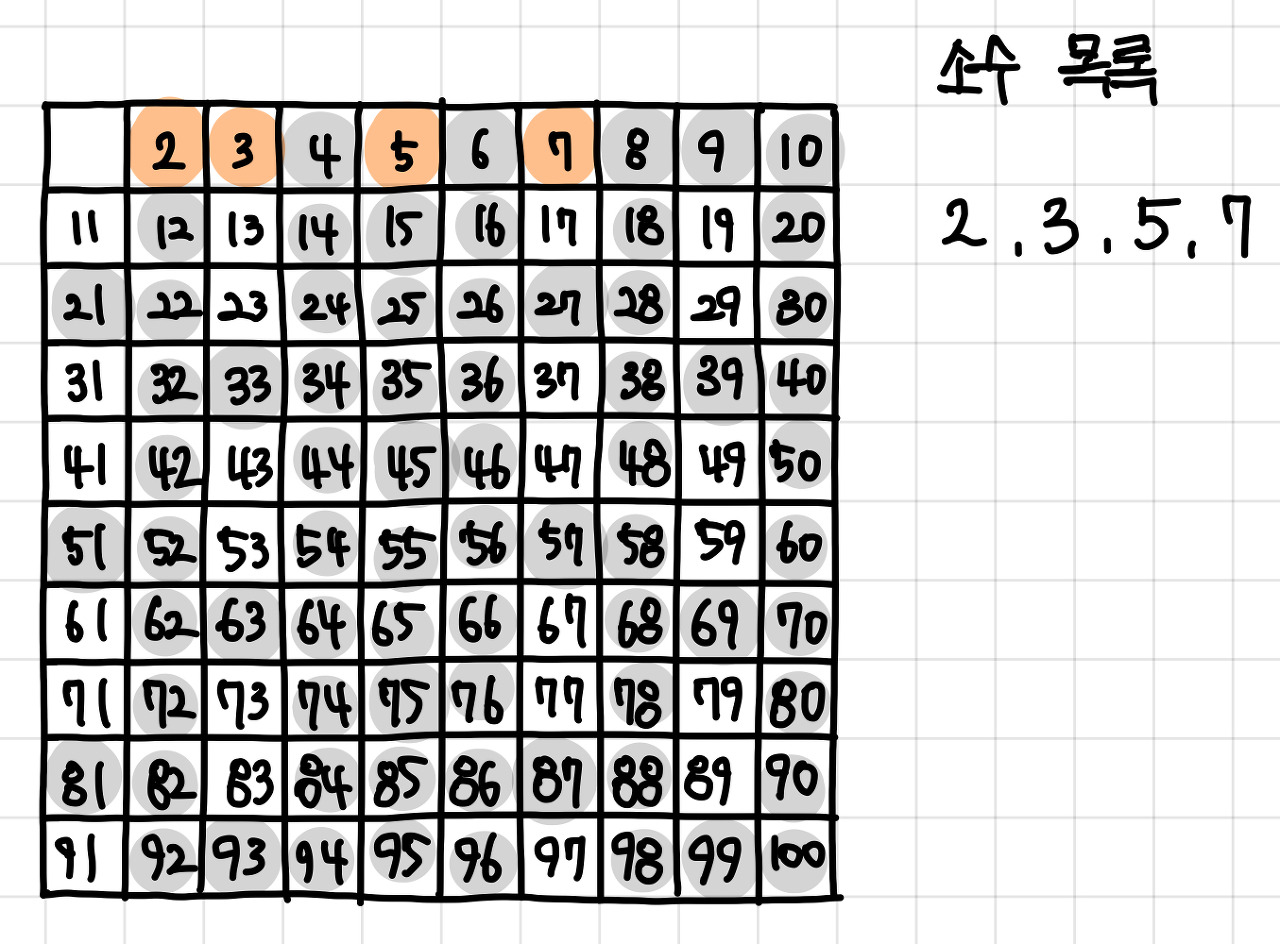
9. 자기 자신을 제외한 7의 배수를 모두 지운다. ▼
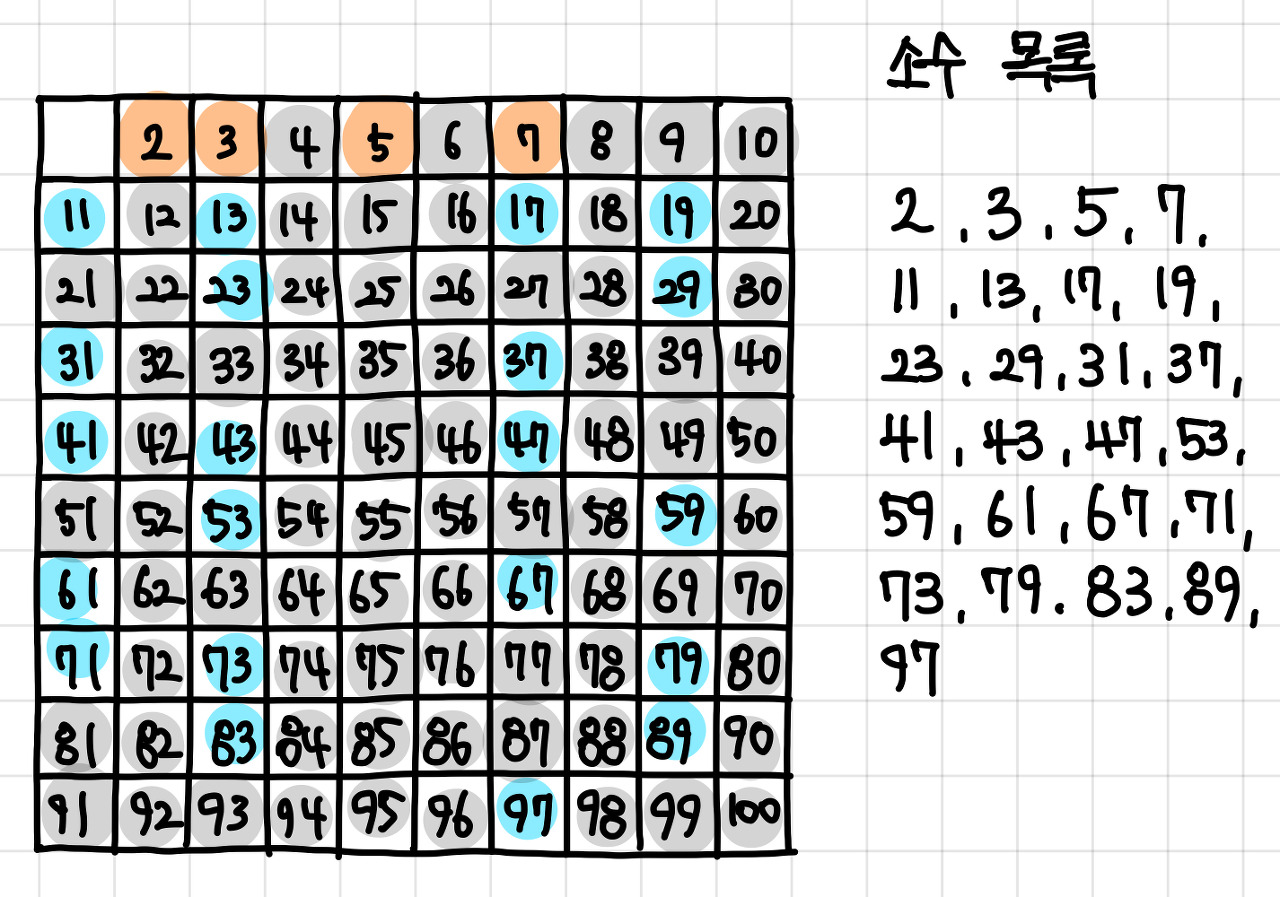
10. 100의 제곱근은 10이므로 10까지 반복해주는데, 7위로는 소수가 없으므로 남은 수들을 세준다. 그 수들이 소수다.
이 과정을 반복하면 구간의 모든 소수를 구할 수 있다.
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 기본적인 자료구조 (0) | 2024.01.27 |
|---|---|
| 배열(array)과 연결 리스트(linked list) (0) | 2024.01.23 |
| 정렬 - 거품 정렬부터 셀 정렬까지 (0) | 2024.01.22 |
| 브루트 포스 (0) | 2024.01.20 |
| 알고리즘과 입출력 (0) | 2024.01.18 |




