

개요
트리(tree) 구조는 그래프의 일종으로, 한 노드에서 시작해서 다른 정점들을 순회하여 자기 자신에게 돌아오는 순환이 없는 연결 그래프이다.
말이 조금 어렵게 되어 있는데, 좀 더 쉽게 말하면 현재 노드를 떠나면 같은 길을 되돌아오는게 아닌 한 현재 노드로 돌아올 수 없다는 것이다.
버스를 탄다고 했을 때, 보통 반대 차선으로 가면 똑같은 버스가 있기 마련인데 가끔 편도로 가는 버스들이 있다.
일단 위의 말이 이해가 안된다면, 트리 구조를 편도로 가는 버스 정도로 이해하고 들어가자.▼
앞에서 트리에 대한 설명으로 `순환이 없는 연결 그래프`라고 했다.
트리와 그래프와는 별개의 자료구조로 느껴지지만, 트리는 따지고 보면 그래프의 한 종류가 될 수 있다.
다만 그 특수성이 짙은 자료구조로서 그래프와 따로 보는 편이다.
트리 구조의 용어
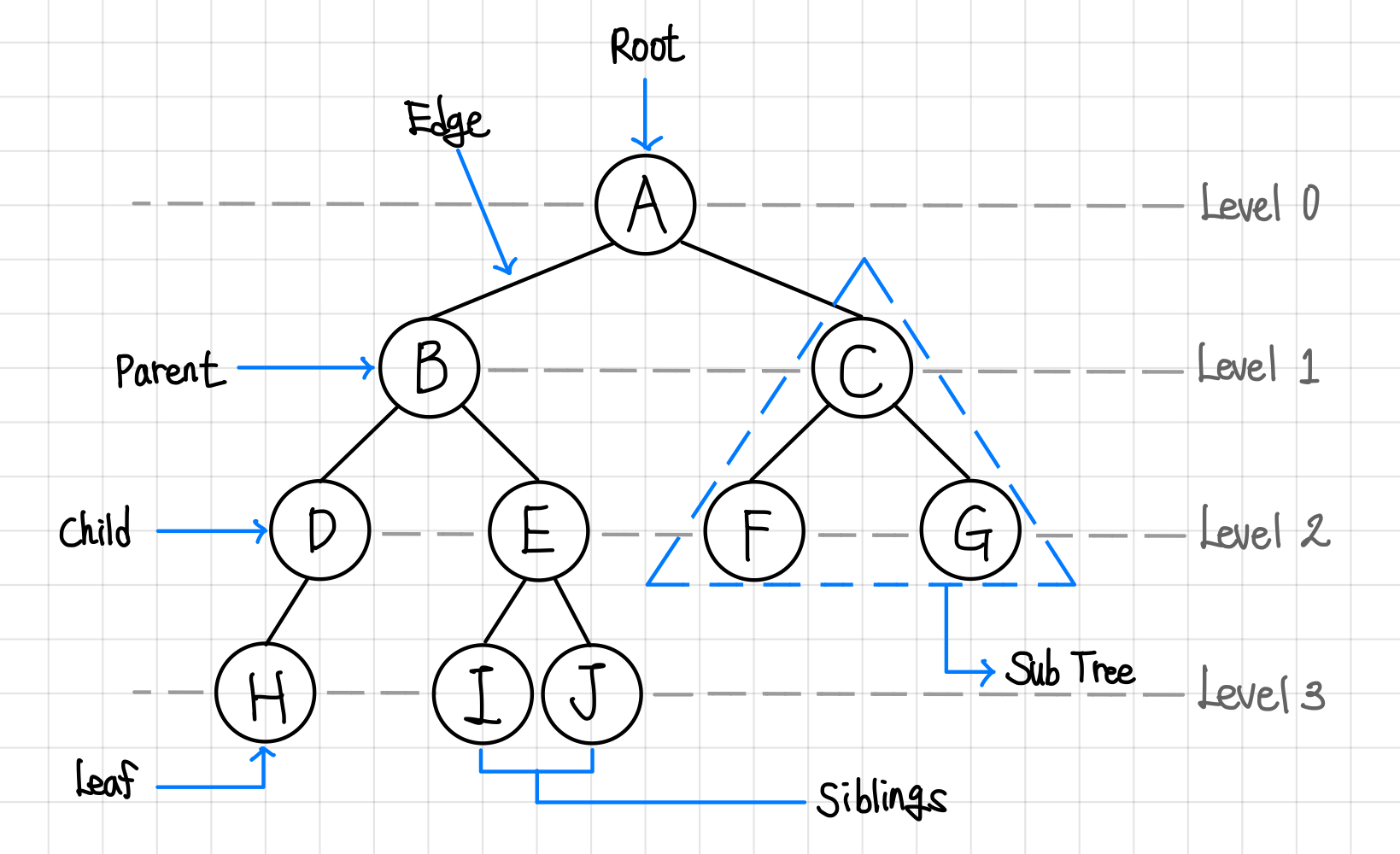
- 노드(Node)
트리를 구성하고 있는 기본적인 요소를 말한다.
노드에는 데이터와 하위 노드를 가리키는 포인터가 있다.
A, B, C, D, E, F, G, H, I, J 가 해당된다. - 간선(Edge)
노드와 노드를 연결하고 있는 연결선을 말한다. - 루트 노드(Root Node)
트리 구조의 부모가 없는 최상위 노드를 말한다.
A 가 해당된다. - 부모 노드(Parent Node)
자식 노드를 가진 노드를 말한다.
A, B, C, D, E 가 해당된다. - 자식 노드(Child Node)
부모 노드의 하위 노드를 말한다.
노드는 부모 노드이면서 동시에 자식 노드일 수 있다.
B, C, D, E, F, G, H, I, J 가 해당된다. - 형제 노드(Sibling Node)
같은 부모 노드를 가지는 노드를 말한다.
D와 E는 부모로 B를 가지는 형제 노드이고, F와 G는 C를, I와 J는 E를 부모로 갖는 형제 노드이다. - 외부 노드(External Node, Outer Node), 단말 노드(Terminal Node), 리프 노드(Leaf Node)
자식 노드가 없는 노드를 말하며, 보통 단말 노드와 리프 노드라고 부른다.
F, G, H, I, J 가 해당된다. - 내부 노드(Internal Node, Inner Node), 비 단말 노드(Non-Terminal Node), 가지 노드(Branch Node)
자식 노드를 하나 이상 가진 노드를 말하며, 보통 가지 노드라고 부른다.
단말 노드가 아닌 모든 노드가 해당된다. - 하위 트리(Sub Tree)
큰 트리(전체)에 속하는 작은 트리들을 말한다. - Level
루트에서 어떤 노드까지의 간선(Edge)의 수를 말한다.
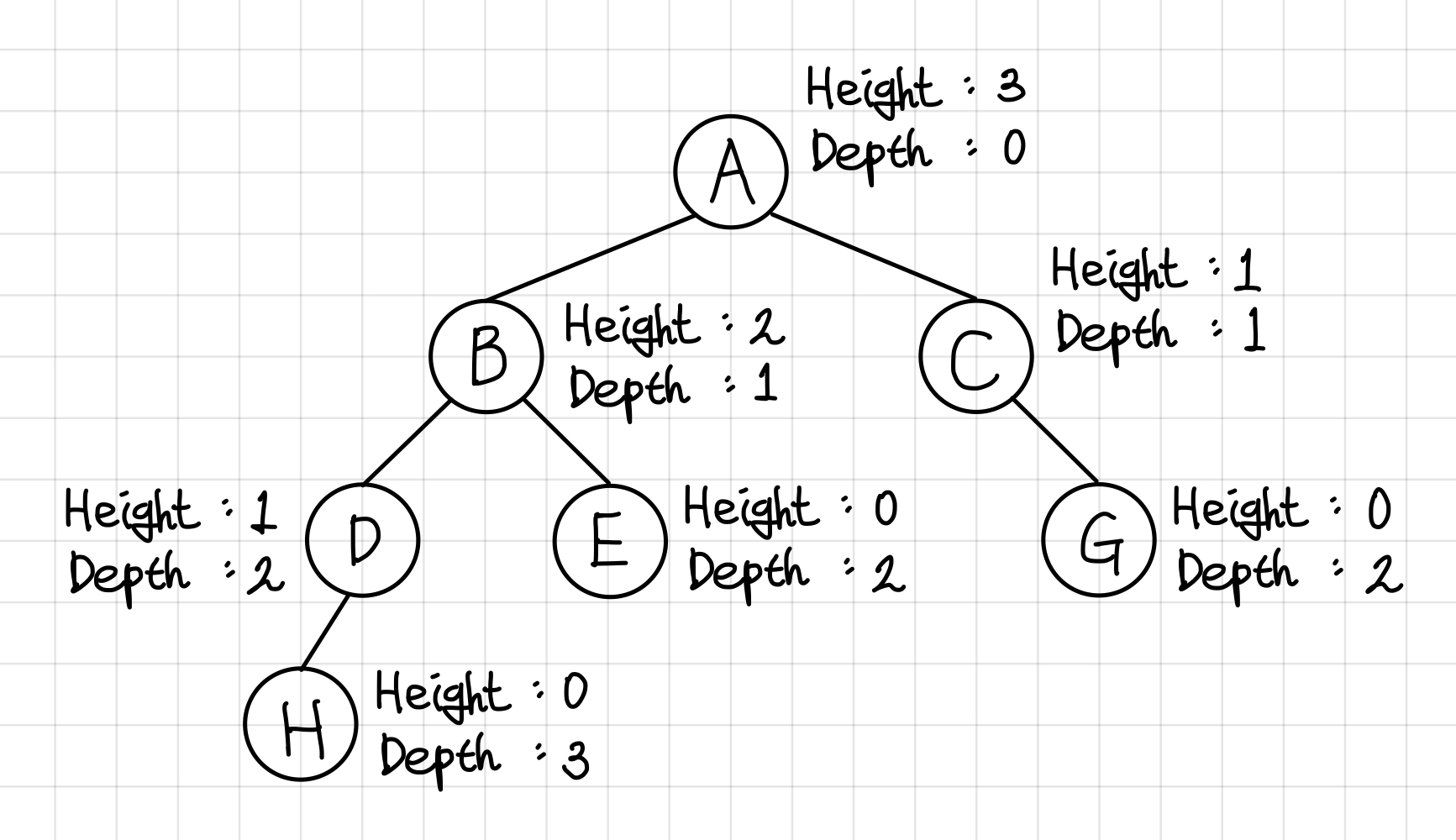
- 깊이(Depth)
루트에서 특정 노드까지의 간선(Edge)수를 말한다. - 높이(Height)
특정 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge)수를 말한다.
트리의 특징
트리는 그래프로 볼 수 있지만 특수성이 짙어 따로 빼서 알아보곤 한다.
그러면 이제 그래프와 구분되는 트리의 특성을 알아보자.
1. 트리는 하나의 루트 노드와 0개 이상의 서브 트리로 구성되어있다.
루트 노드는 하나만 존재한다.
만약에 아래와 같은 트리가 있다면, 이는 트리가 아니거나 각각을 별개의 트리로 본다.▼
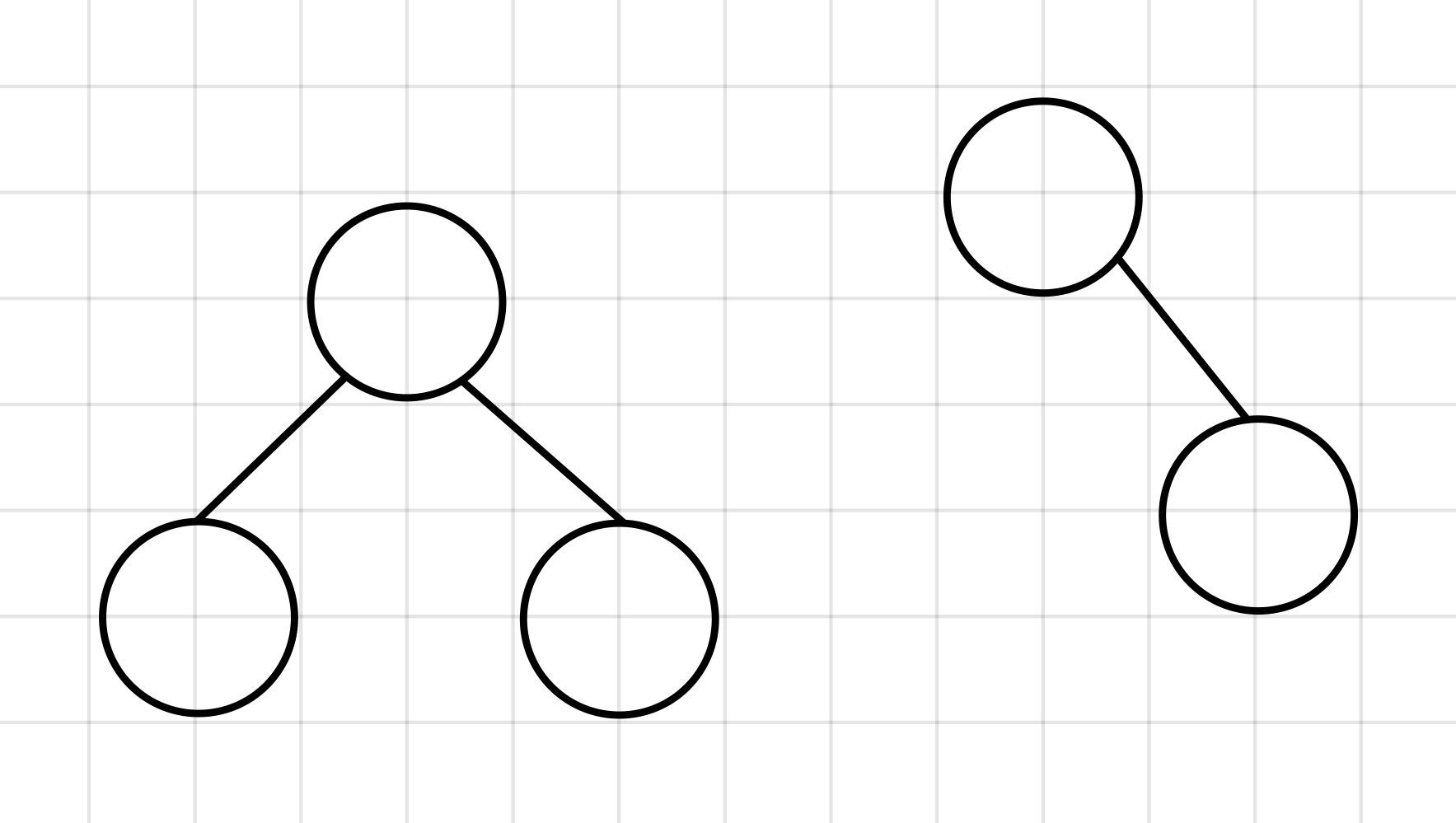
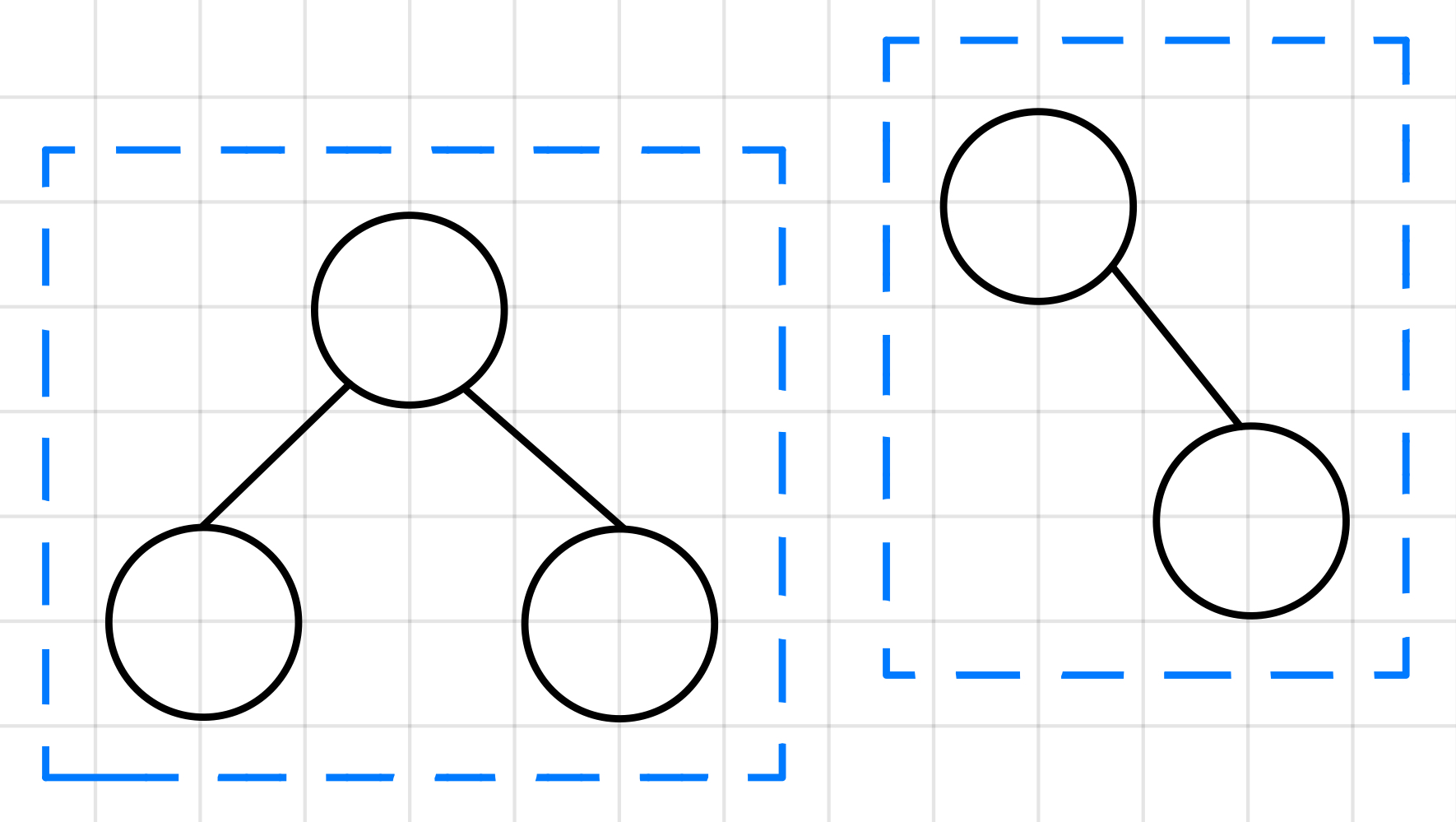
2. 데이터를 순차적으로 저장하지 않는 비선형 자료구조이다.
스택, 큐, 덱, 배열, 연결리스트는 데이터를 순차적으로 저장하지만 트리는 데이터를 어떻게 순회하느냐에 따라 순서가 달라진다.
3. 단순 순환(Loop 또는 Cycle)을 갖지 않는 무방향 연결 그래프 구조이다.
앞에서 언급한 대로, 트리는 순환을 갖지 않는다.
이는 형제 노드끼리 연결되지 않는다는 반증도 된다.
왔던 경로를 되돌아가지 않는한, 원래 위치로 되돌아 갈 수 없는 구조이다.
4. 부모 자식 관계를 갖고 있는 계층형 자료구조이다.
엄격한 부모 자식 관계를 갖고 있다.
그래프와 트리를 구분짓는 핵심적인 특성으로, 부모 자식 관계를 통해 계층화를 한다.
5. 모든 자식 노드는 하나의 부모 노드만 갖는다.
부모 노드를 둘 갖는 자식 노드는 3번째 특성을 해치게 된다.
아래의 그림을 보면, 딱 보기에도 트리가 아니지만, 갔던 경로를 되돌아오지 않고도 원래 노드에 도달할 수 있게 된다.▼
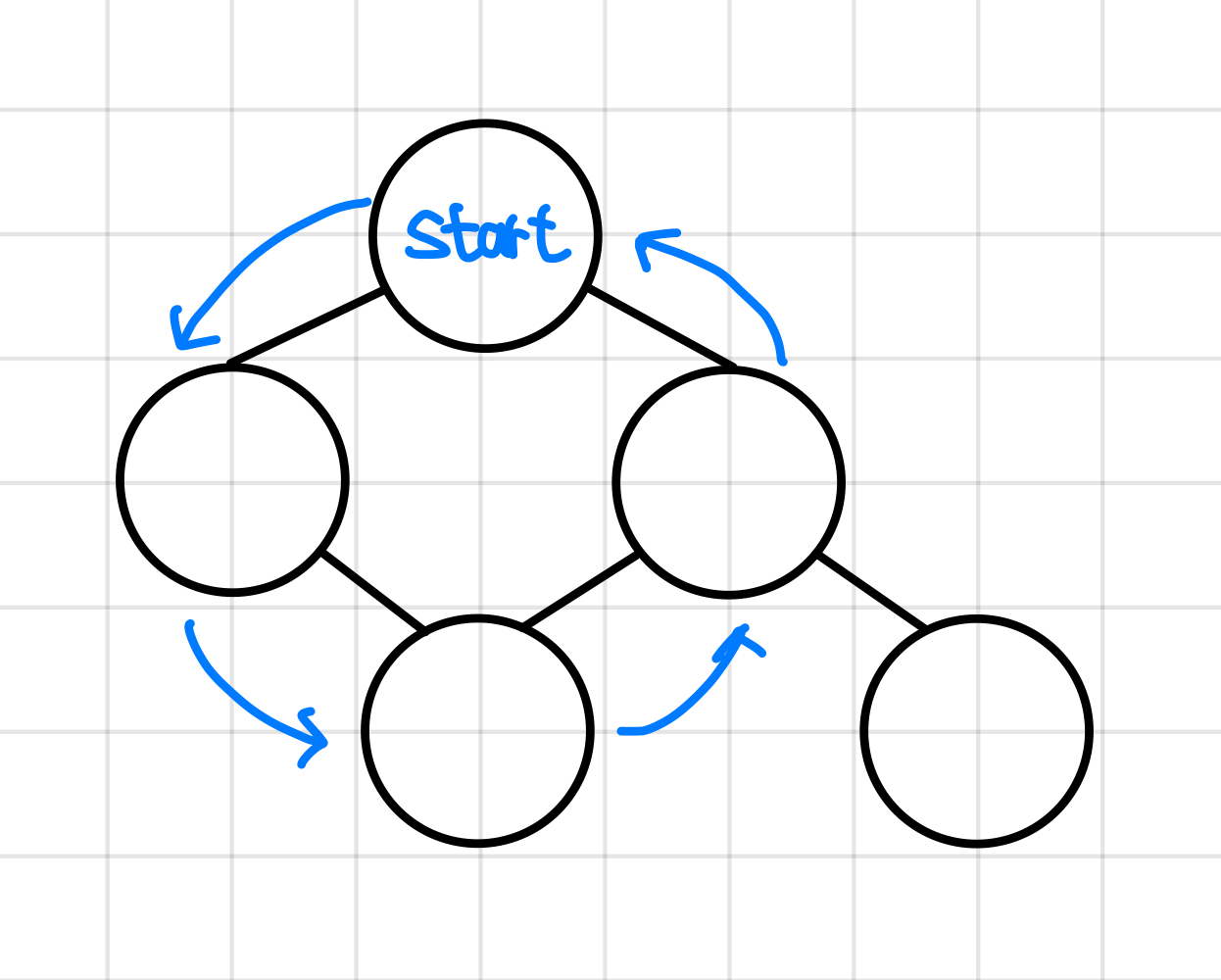
6. N개의 노드가 있다고 하면 간선은 항상 N - 1개 이다.
순환이 형성되지 않는다면, 간선은 언제나 N - 1개가 된다.
이 개념은 최소 신장 트리에서도 나온다.
트리의 종류
트리에는 여러가지 종류가 존재한다.
일부는 굉장히 단순한 형태를 갖고 있지만, 그 외의 다른 트리들은 복잡한 구조를 지니고 있고 이를 활용하거나 연구하는 논문들도 굉장히 많다.
여기서는 최대한 넓고 얕게 보는 것으로 하자.
편향 트리(Skew Tree)
편향 트리는 모든 노드들이 자식을 하나만 가진 트리를 말한다.
그림으로 보면 굉장히 쉽게 이해된다.▼
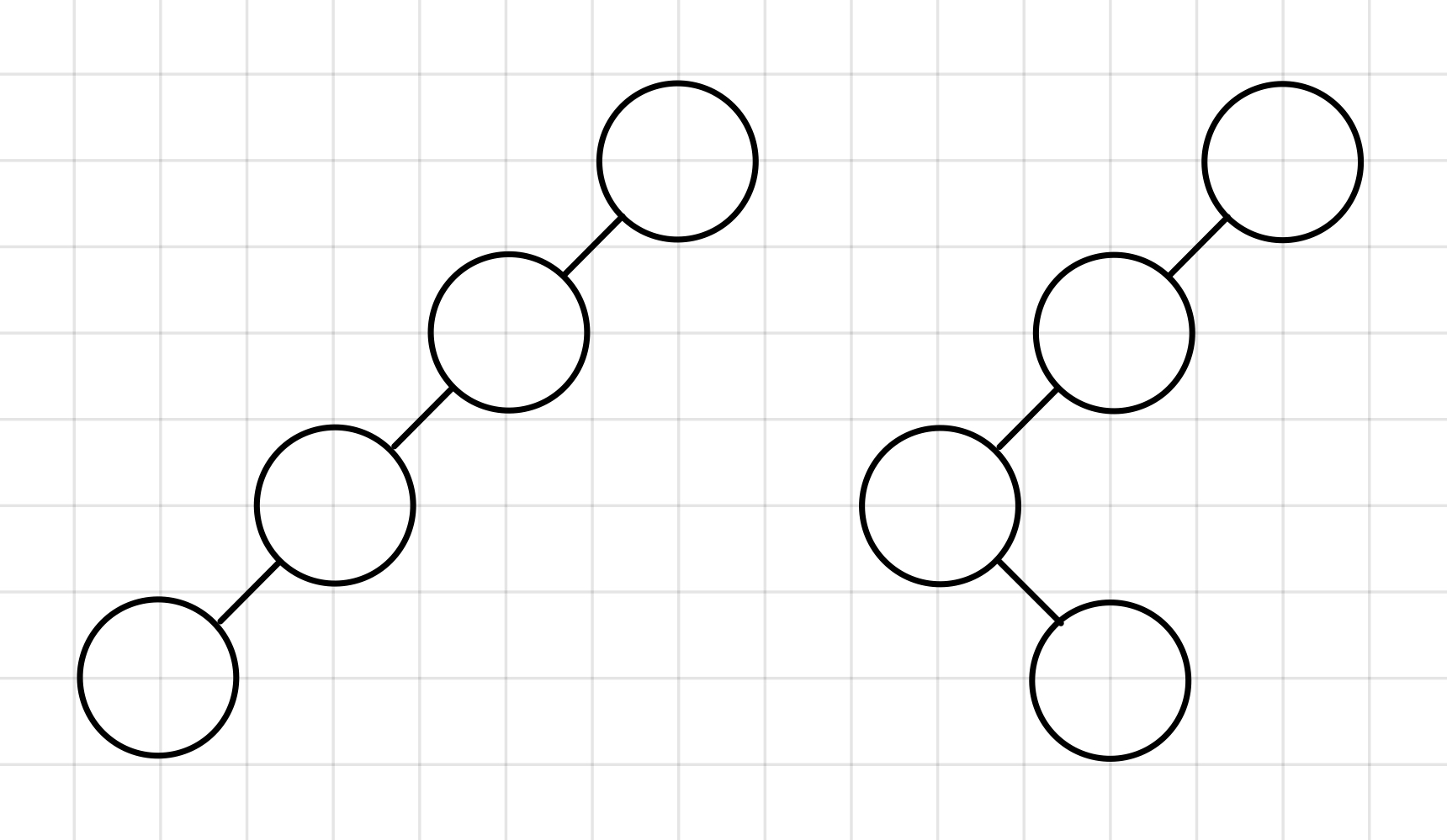
이진 트리(Binary Tree)
이진 트리는 각 부모 노드의 자식 노드의 개수가 2 이하인 트리이다.
이진트리가 되려면, 루트 노드를 중심으로 둘로 나뉘는 두 개의 서브 트리도 이진 트리이어야 하고, 그 서브 트리의 모든 서브 트리도 이진 트리이어야 한다.▼
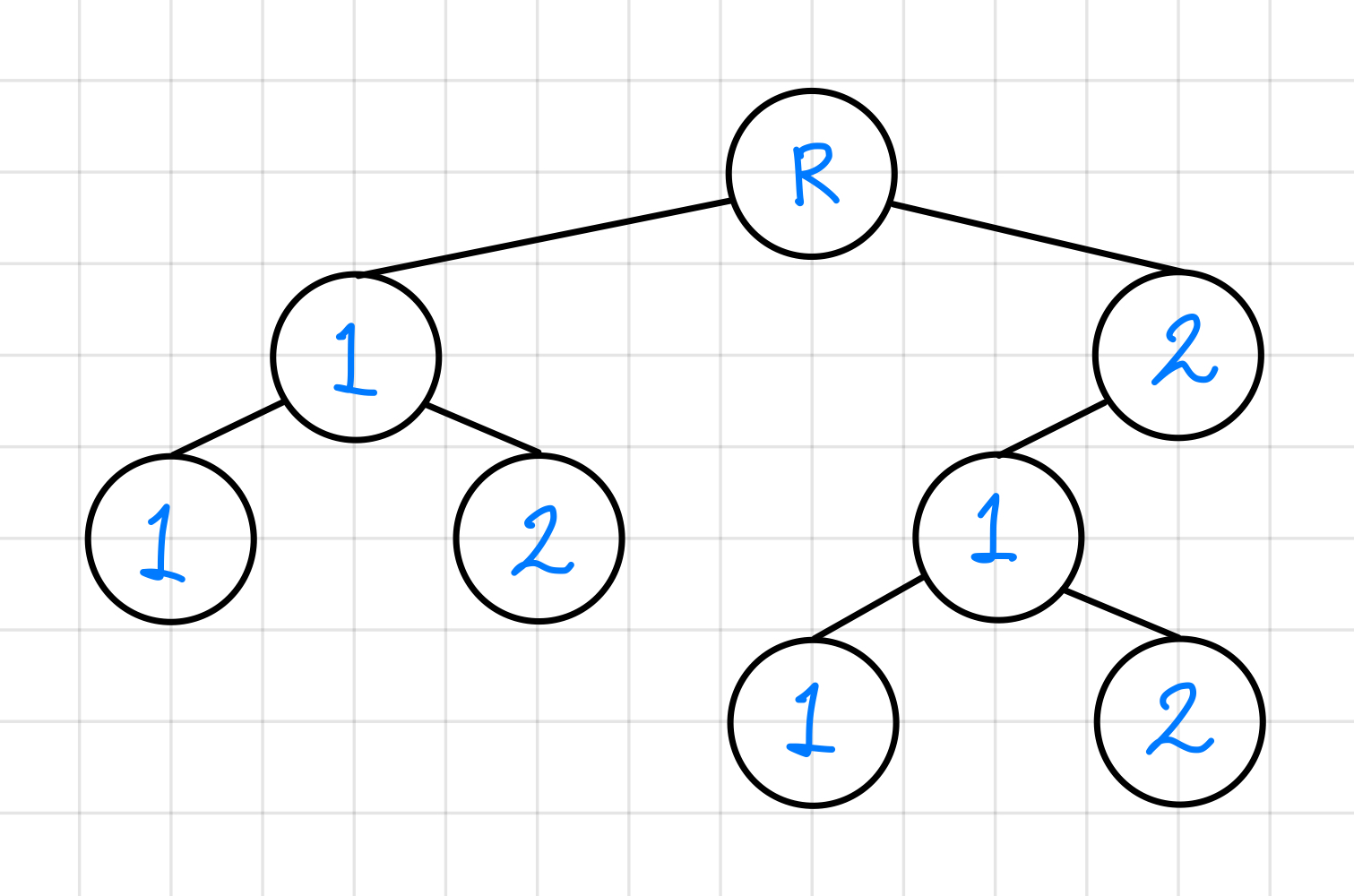
이진 트리는 두 가지 특성으로 나눌 수 있다.
하나는 포화 이진 트리(Full Binary Tree), 다른 하나는 완전 이진 트리(Complete Binary Tree)이다.
포화 이진 트리(Full Binary Tree)
포화 이진 트리는 모든 잎의 레벨이 동일한 이진 트리이며, 잎이 아닌 내부 노드들은 모두 2개의 자식을 가지는 트리를 말한다.
잎이 아닌 내부 노드들이 모두 2개의 자식을 가져야 하므로, 한 레벨이 생기게 되면 그 레벨은 항상 꽉 차게 된다.
그렇기에 포화 이진 트리는 아래와 같은 형태를 갖게 되고, 모든 레벨이 2의 제곱수의 노드를 갖게 되므로 노드의 개수는 $$ 2^{height}-1 $$ 이 된다.▼
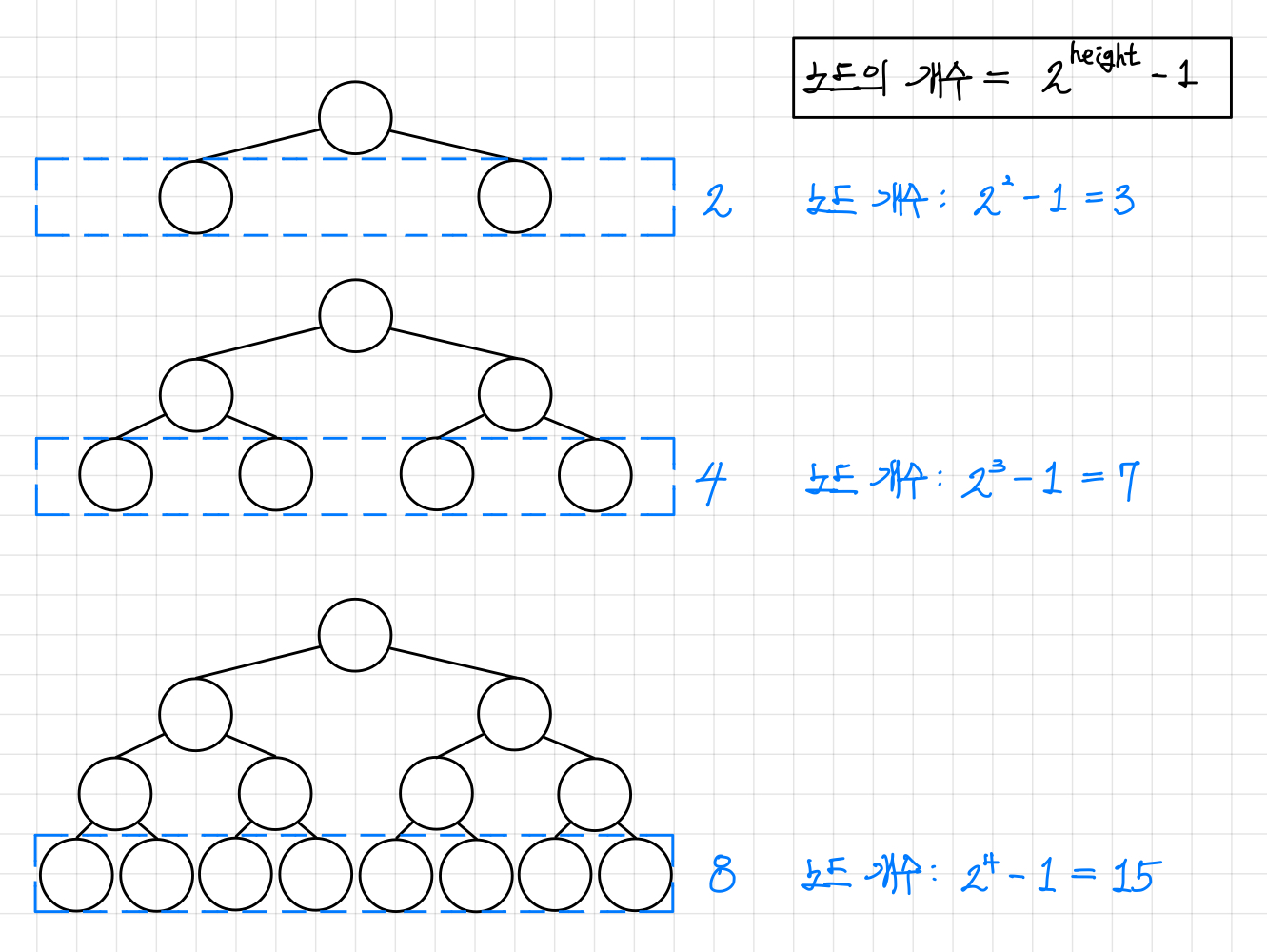
완전 이진 트리(Complete Binary Tree)
완전 이진 트리는 포화 이진 트리에서 오른쪽 리프부터 제거해 나간 트리를 말한다.▼
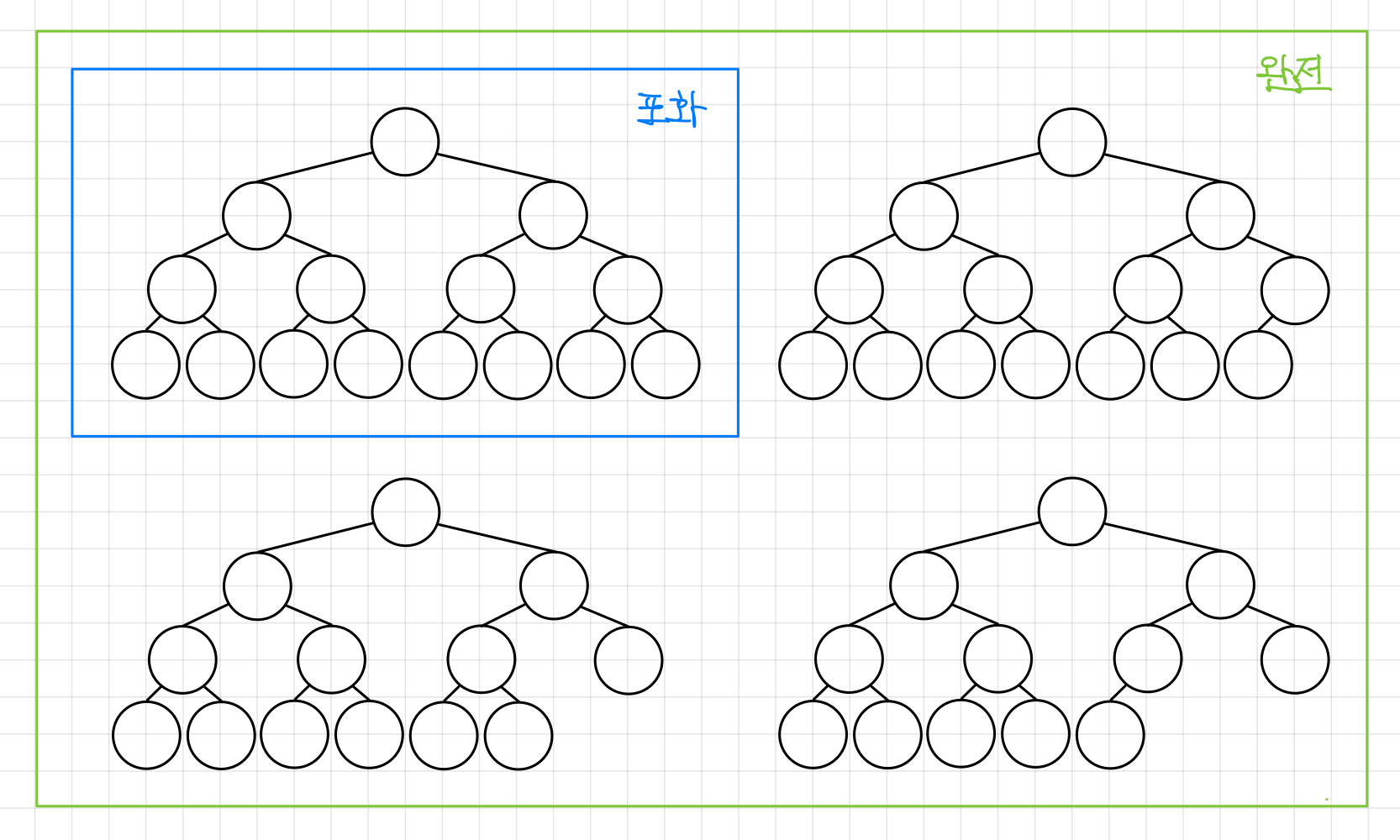
포화 이진 트리도 완전 이진 트리에 속한다.
이진 탐색 트리(Binary Search Tree, BST)
이진 탐색 트리는 순서화 된 이진 트리로, 노드의 왼쪽 자식은 부모의 값보다 작고 오른쪽 자식은 부모의 값보다 큰 이진 트리이다.▼
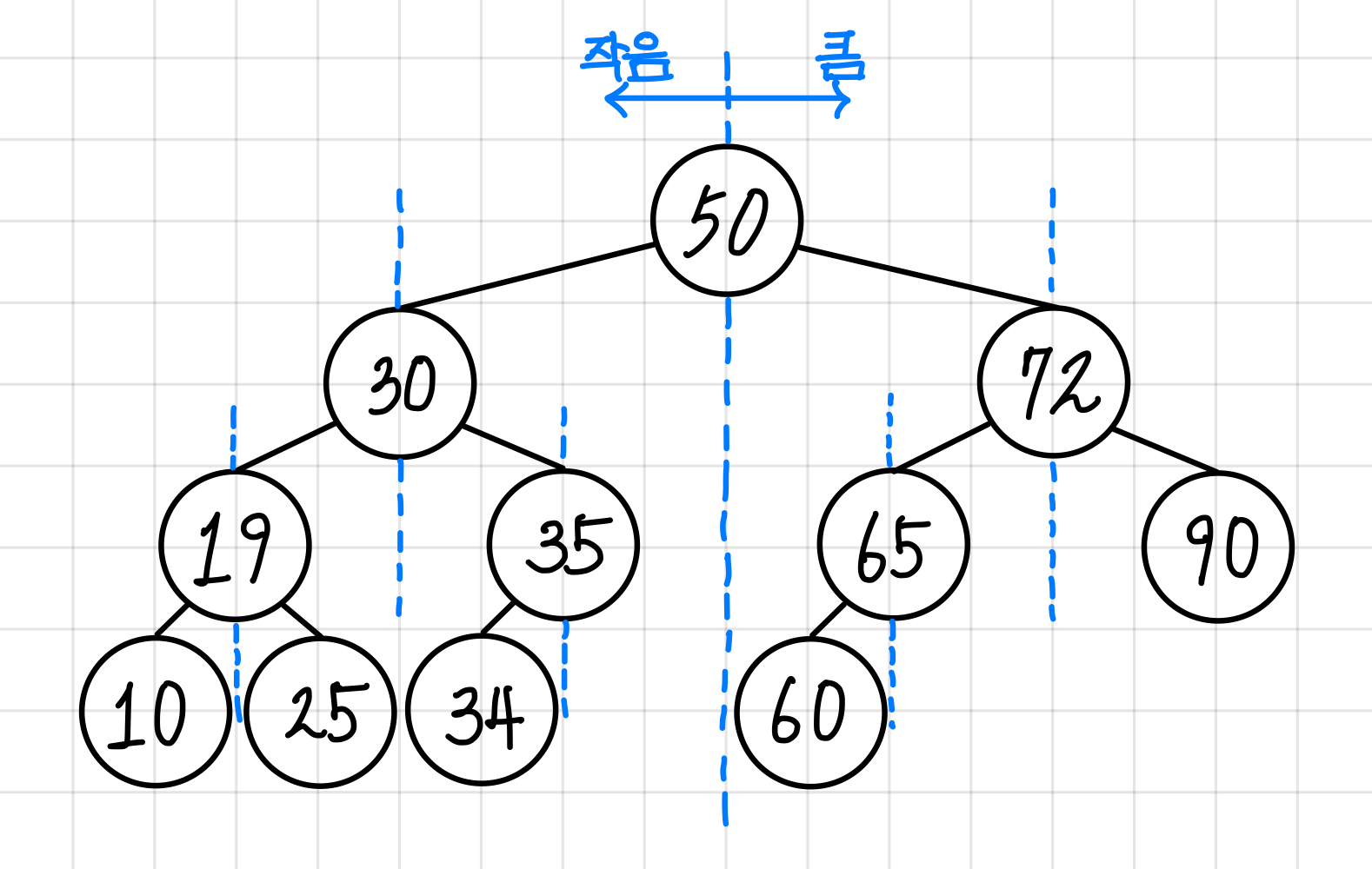
이진 탐색과 이진 트리가 합쳐졌다고 생각하면 쉽다.
이진 탐색 트리는 나중에 별도의 글로 다루겠다.
B-Tree
B-Tree는 이진 트리를 확장한 것으로 자식 노드를 2개까지만 가질 수 있는 이진 트리와는 다르게 B-Tree는 2개 이상을 가질 수 있다.
B-Tree는 데이터베이스와 하드 디스크의 파일 시스템과 같은 곳에서 널리 사용된다.
"자식 노드를 2개 이상을 갖는 트리면 그냥 일반적인 트리가 아닌가요?"
B-Tree의 기본 개념은 내부 노드의 자식 노드의 수가 미리 정해진 범위 내에서 변경이 가능하다는 것이다.
무한정 원하는 만큼 넣고, 빼는게 아니라 범위가 정해져 있다는 것에서 우리가 생각하는 일반적인 트리와는 다르다.
게다가 데이터가 추가되거나 제거 될 때 내부 노드는 정해진 범위의 자식 노드 수를 맞추기 위해 분리 또는 결합이 이루어진다.
일단은 이런 특징을 가진 트리인데, 더 자세한 내용을 다루기엔 내용이 많이 길어질 것 같아서 B-Tree도 다른 글에서 다루기로 하겠다.
트리의 순회
트리의 순회라고는 했지만 엄밀히 말하자면 이진 트리의 순회이다.
이진 트리의 순회는 크게 세 종류가 있다.
전위 순회(Preorder Traverse), 중위 순회(Inorder Traverse) 그리고 후위 순회(Postorder Traverse)이다.
아래의 트리를 예시로 세 가지 순회를 살펴보자.▼
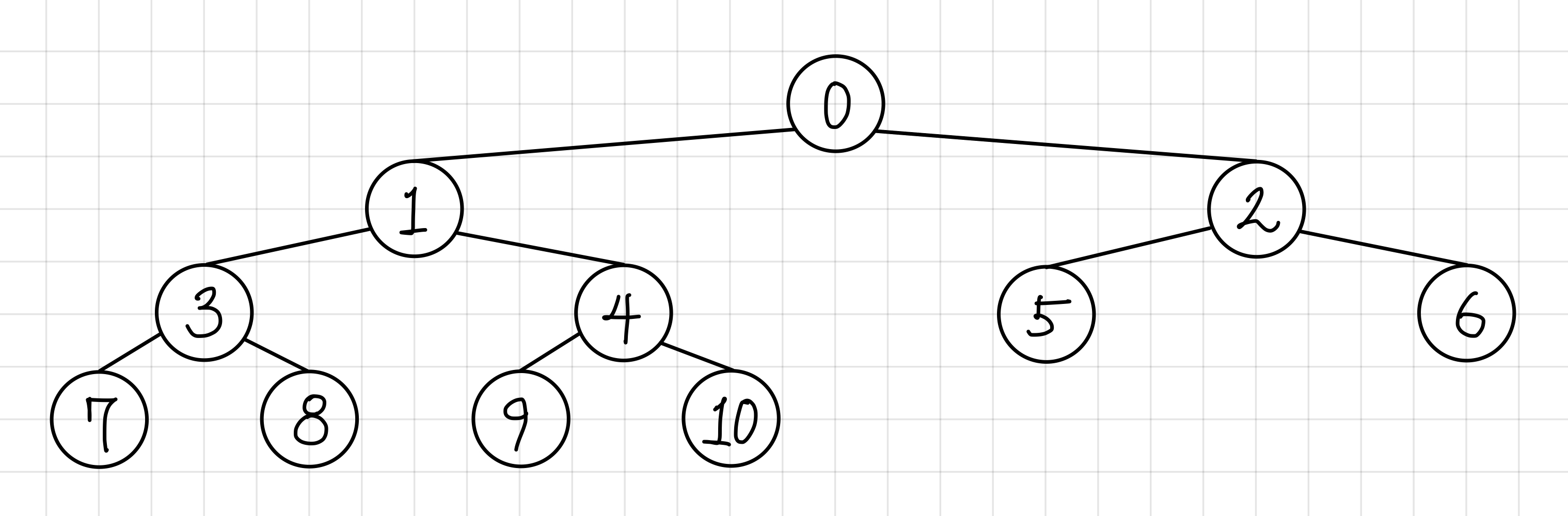
전위 순회(Preorder Traverse)
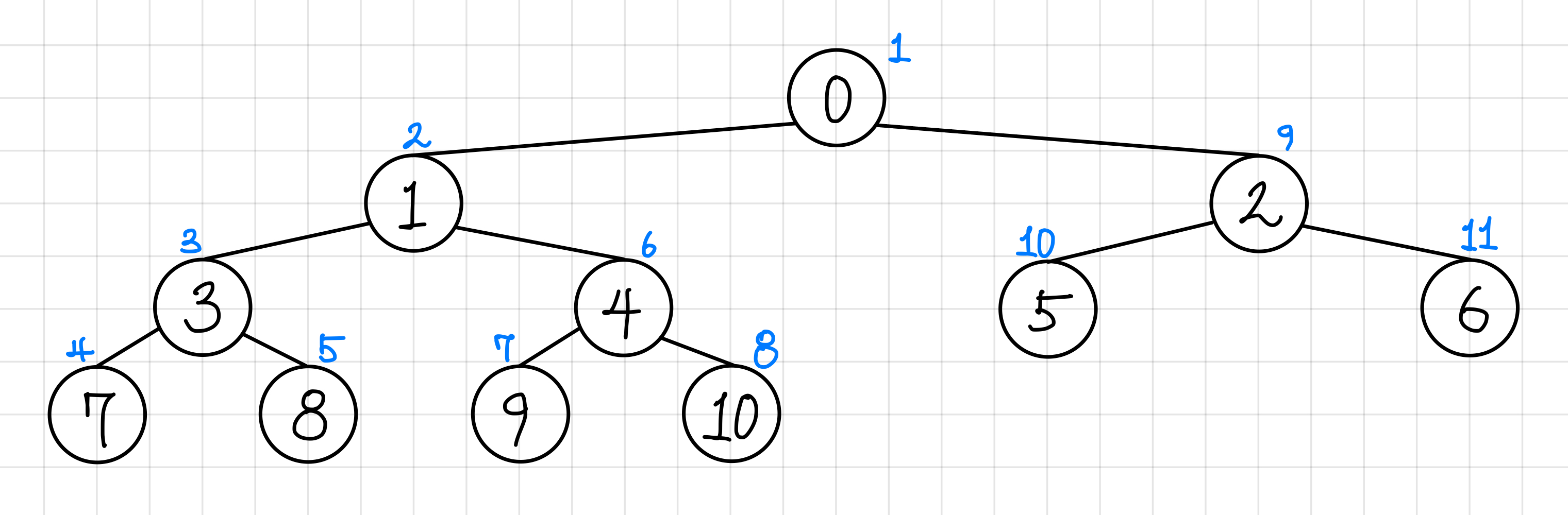
전위 순회는 루트부터 먼저 방문하는 순회 방식이다.
먼저 루트를 방문 한 후, 그 다음 왼쪽 하위 트리의 루트를 방문하고 더 이상 방문할 왼쪽 하위 트리가 없다면 그 때부터 오른쪽 하위 트리를 방문하는 방식이다.
이 방식대로 순회하게 되면,
0, 1, 3, 7, 8, 4, 9, 10, 2, 5, 6 의 순서로 순회하게 된다.▼
중위 순회(Inorder Traverse)
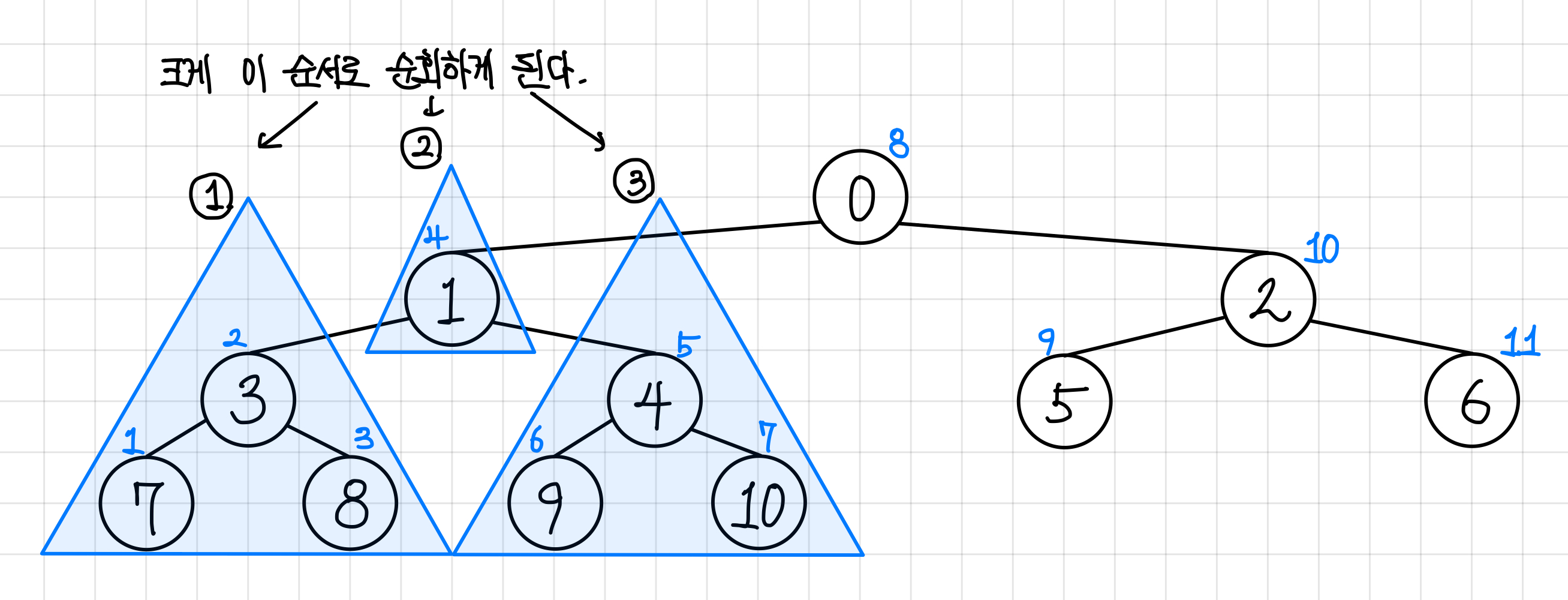
중위 순회는 왼쪽 하위 트리를 방문한 후 루트를 방문하는 순회 방식이다.
가장 왼쪽 하위 트리를 먼저 방문한 뒤에, 해당 하위 트리의 루트에 방문하고 오른쪽 트리를 방문하는 식이다.
이 방식대로 순회하게 되면,
7, 3, 8, 1, 9, 4, 10, 0, 5, 2, 6 의 순서로 순회하게 된다.▼
후위 순회(Postorder Traverse)
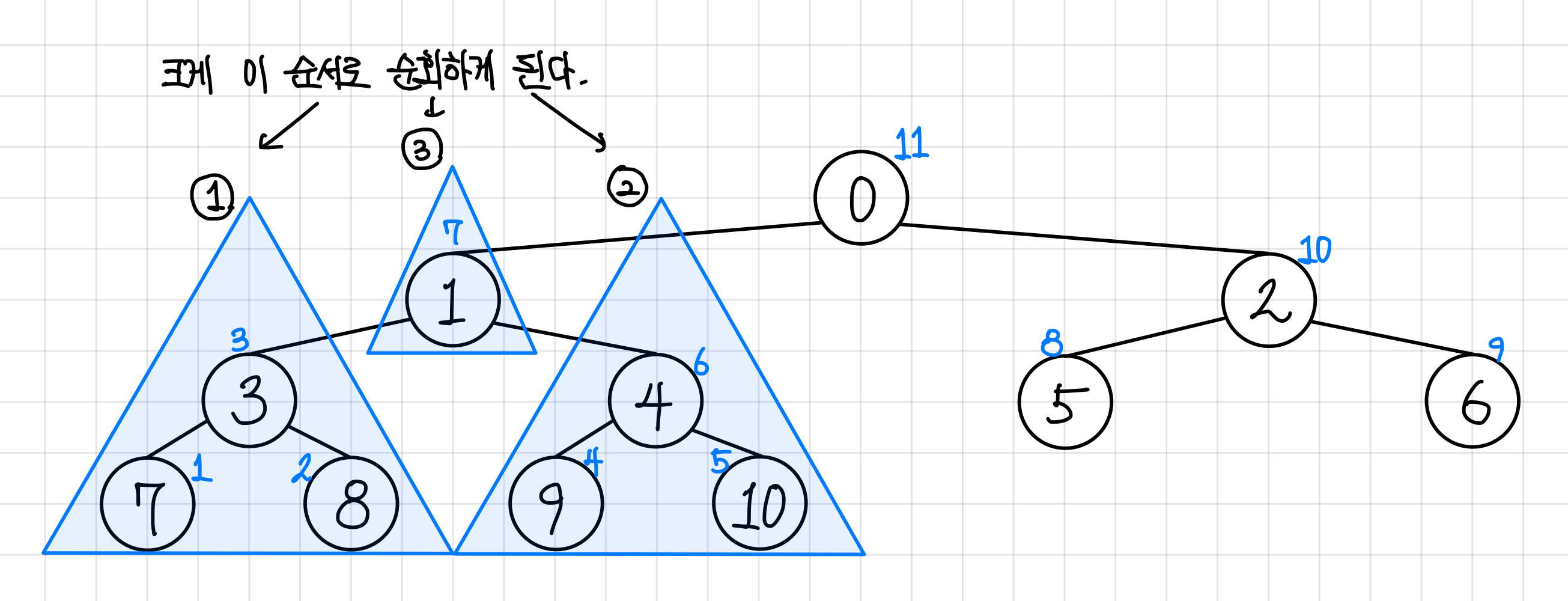
후위 순회는 하위 트리를 모두 방문한 후 루트를 방문하는 순회 방식이다.
왼쪽 하위 트리부터 하위 트리를 모두 방문 한 후에 루트를 방문하는 식이다.
이 방식대로 순회하게 되면,
7, 8, 3, 9, 10, 4, 1, 5, 6, 2, 0 의 순서로 순회하게 된다.▼
트리와 그래프의 차이
마지막으로 트리를 그래프로 볼 수 있다고 했는데, 어떤 차이로 그래프와 따로 보는 지 확인해보자.
| 그래프 | 트리 | |
| 정의 | 노드와 그 노드를 연결하는 간선을 하나로 모아 놓은 자료구조. | 그래프의 한 종류. DAG(Directed Acyclic Graph)의 한 종류. |
| 방향성 | 방향 그래프, 무방향 그래프 모두 존재. | 방향 그래프(Directed Graph). |
| 싸이클 | 싸이클(Cycle) 가능. 자체 간선(Self-loop) 가능. 순환 그래프, 비순환 그래프 모두 존재. |
싸이클 불가능. 자체 간선 불가능. 비순환 그래프만 존재. |
| 루트 노드 | 루트 노드의 개념 없음. | 한 개의 루트 노드만이 존재. |
| 부모-자식 | 부모-자식 개념이 없음. | 모든 자식 노드는 한 개의 부모 노드만을 가짐. top-bottom 또는 bottom-top 으로 이루어짐. |
마치며
트리 구조는 굉장히 중요한 구조이다.
우리가 사용하는 컴퓨터의 파일 구조도 트리 구조로 되어있고, 현실 세계의 계층 모델들도 트리로 쉽게 구현할 수 있다.
알고리즘적으로도 중요하고, 자료구조적으로도 중요하기에 트리에 대해서 좀 더 깊게 알 필요가 있다고 생각된다.
'Algorithm > Algorithm 개념' 카테고리의 다른 글
| 다이나믹 프로그래밍 (0) | 2024.02.07 |
|---|---|
| 분할 정복 (0) | 2024.01.27 |
| 기본적인 자료구조 (0) | 2024.01.27 |
| 배열(array)과 연결 리스트(linked list) (0) | 2024.01.23 |
| 정렬 - 거품 정렬부터 셀 정렬까지 (0) | 2024.01.22 |




