

문제
오늘도 서준이는 깊이 우선 탐색(DFS) 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자.
N개의 정점과 M개의 간선으로 구성된 무방향 그래프(undirected graph)가 주어진다. 정점 번호는 1번부터 N번이고 모든 간선의 가중치는 1이다. 정점 R에서 시작하여 깊이 우선 탐색으로 노드를 방문할 경우 노드의 방문 순서를 출력하자.
깊이 우선 탐색 의사 코드는 다음과 같다. 인접 정점은 오름차순으로 방문한다.
dfs(V, E, R) { # V : 정점 집합, E : 간선 집합, R : 시작 정점
visited[R] <- YES; # 시작 정점 R을 방문 했다고 표시한다.
for each x ∈ E(R) # E(R) : 정점 R의 인접 정점 집합.(정점 번호를 오름차순으로 방문한다)
if (visited[x] = NO) then dfs(V, E, x);
}
입력
첫째 줄에 정점의 수 N (5 ≤ N ≤ 100,000), 간선의 수 M (1 ≤ M ≤ 200,000), 시작 정점 R (1 ≤ R ≤ N)이 주어진다.
다음 M개 줄에 간선 정보 u v가 주어지며 정점 u와 정점 v의 가중치 1인 양방향 간선을 나타낸다. (1 ≤ u < v ≤ N, u ≠ v) 모든 간선의 (u, v) 쌍의 값은 서로 다르다.
출력
첫째 줄부터 N개의 줄에 정수를 한 개씩 출력한다. i번째 줄에는 정점 i의 방문 순서를 출력한다. 시작 정점의 방문 순서는 1이다. 시작 정점에서 방문할 수 없는 경우 0을 출력한다.
문제 링크
https://www.acmicpc.net/problem/24479
풀이
문제에 나와있다시피, DFS를 이용해야한다.
DFS는 깊이우선탐색으로 가장 우선순위가 높고 인접한 정점으로 계속해서 이동시키면 된다.
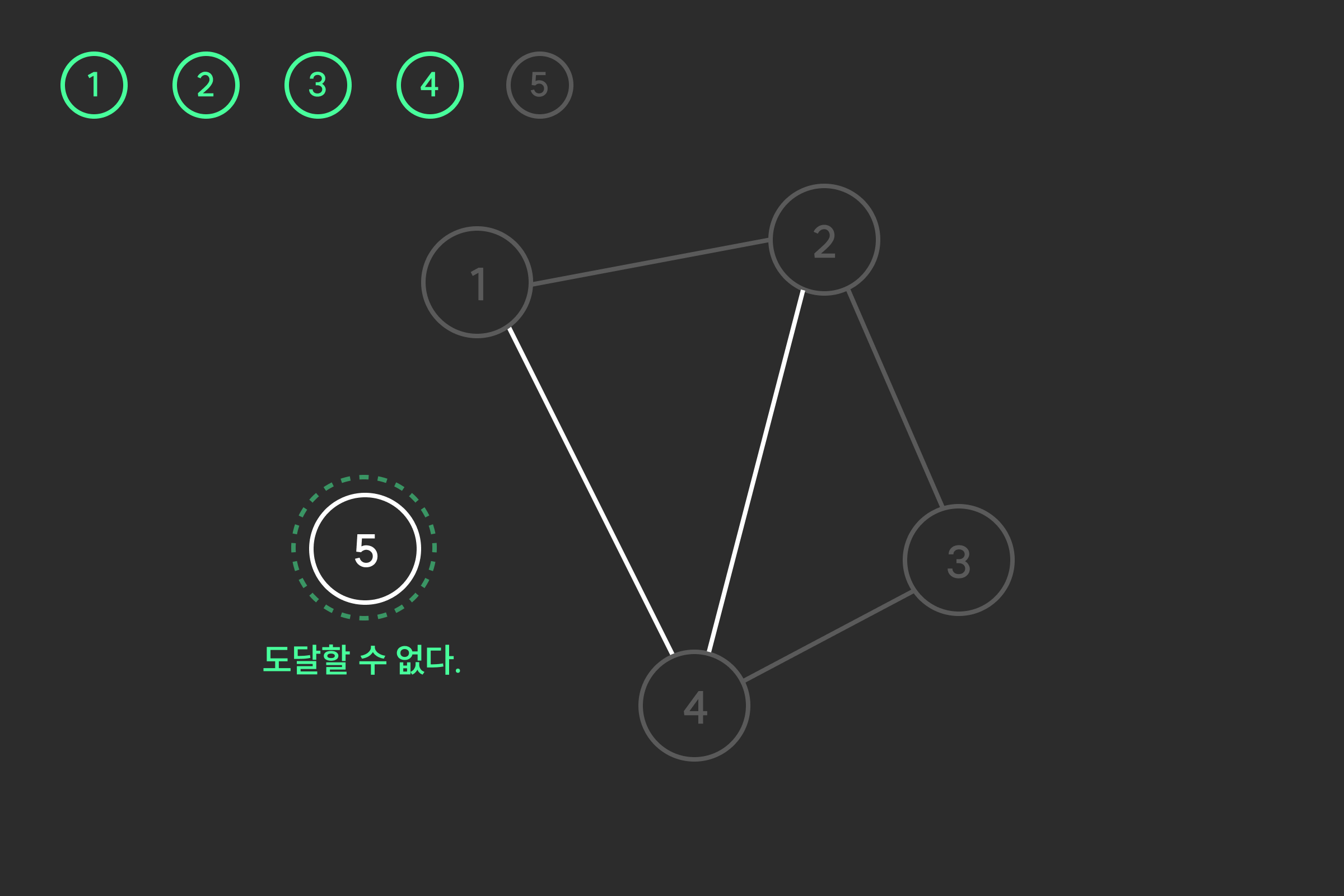
아래와 같이 정점과 간선이 있다고 해보자. ▼

시작점이 1이라고 했으니, 1번 정점부터 방문하게 된다. ▼

방문한 지점은 방문했다고 체크를 해두고, 갈 수 있는 다음 정점을 찾아본다.
갈 수 있는 다음 정점은 2와 4가 있는데, 이 중 숫자가 더 작은 2부터 방문한다. ▼

똑같이 2번도 방문했다고 체크를 해두고, 갈 수 있는 다음 정점들을 찾아본다.
인접한 정점들로는 1, 3, 4가 있는데 1은 이미 방문했으니 넘기고, 방문하지 않은 정점들 중 가장 작은 3번 정점으로 향한다. ▼

3번 정점은 방문했으니 방문했다고 체크를 하고, 인접한 정점들을 확인해본다.
2번과 4번이 있으나 2번은 이미 방문을 했으니 4번 정점으로 향한다. ▼

이제 모두 방문을 했으니 더 이상 갈 수 없어져 탐색이 종료되고, 5번은 갈 수 없는 것으로 결론을 내린다. ▼
"이론은 쉬운데... 코드를 어떻게?"
사실 차근차근 따라가면 이론 자체는 굉장히 쉽다.
- 갈 수 있는 곳들을 우선 기록
- 그 중에서 가장 먼저 갈 수 있는 곳을 탐색
- 쭉 탐색하다가 더 이상 갈 수 없다고 판단되면 1번에 기록했던 곳들을 다시 확인
- 정말로 갈 수 있는데가 없으면 탐색 종료
"어떻게 짜야할 지 감이 안잡히는데..."
처음에는 감조차도 안잡히는게 당연하다.
DFS를 짜는 방법은 여러가지가 있는데, 가장 대표적인 방법을 소개하자면 재귀다.
재귀를 사용해 DFS를 구현하게 되면 대략적으로 이런 구조를 가지고 있게 된다.

재귀를 사용하지 않고 스택과 반복문을 사용하는 코드도 있으나, 상당히 복잡해지기에 대부분 재귀적으로 해결한다.
위의 형태에 문제에서 요구하는 부분을 추가로 구현해주면 쉽게 해결할 수 있다.
Swift 코드
let NMR = readLine()!.split(separator: " ").map { Int(String($0))! }
let N = NMR[0], M = NMR[1], R = NMR[2]
var graph = Array(repeating: [Int](), count: 100001)
var visit = Array(repeating: 0, count: 100001)
var cnt = 0
var answer = ""
for _ in 0..<M {
let uv = readLine()!.split(separator: " ").map { Int(String($0))! }
let u = uv[0], v = uv[1]
graph[u].append(v)
graph[v].append(u)
}
for i in 0..<100001 {
if graph[i].count > 1 {
graph[i] = graph[i].sorted(by: <)
}
}
func dfs(_ node: Int) {
if visit[node] != 0 {
return
}
cnt += 1
visit[node] = cnt
for i in 0..<graph[node].count {
dfs(graph[node][i])
}
}
dfs(R)
for i in 1...N {
answer += "\(visit[i])\n"
}
print(answer)
C++ 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M, R, cnt;
vector<int> G[100001];
int V[100001];
void dfs(int node) {
if (V[node] != 0) {
return ;
}
V[node] = ++cnt;
for (int i = 0; i < G[node].size(); i++) {
dfs(G[node][i]);
}
}
int main() {
scanf("%d %d %d", &N, &M, &R);
while (M--) {
int A, B;
scanf("%d %d", &A, &B);
G[A].push_back(B);
G[B].push_back(A);
}
for (int i = 1; i <= N; i++) {
sort(G[i].begin(), G[i].end());
}
dfs(R);
for (int i = 1; i <= N; i++) {
printf("%d\n", V[i]);
}
}
C++의 경우 `cin`과 `cout`을 사용하면 시간초과가 난다.
`cin.tie(0)`과 `cout.tie(0)`를 해줘도 시간초과가 계속 나길래 `scanf`와 `printf`를 사용하여 겨우 해결했다.
'Algorithm > PS' 카테고리의 다른 글
| 백준 2805번 나무 자르기 - C++, SWIFT (2) | 2024.11.02 |
|---|---|
| 백준 24444번 알고리즘 수업 - 너비 우선 탐색 1 - C++, SWIFT (0) | 2024.11.01 |
| 프로그래머스 입국심사 - C++ (0) | 2024.10.30 |
| 백준 11561번 징검다리 - C++ (4) | 2024.10.29 |
| 백준 1072번 게임 - C++ (2) | 2024.10.28 |




