

문제
은진이는 지금 (X, Y)에 있고, (0, 0)에 있는 집으로 가능한 빨리 가려고 한다. 이동할 수 있는 방법은 다음 두 가지이다.
첫 번째 방법은 걷는것이다. 걸을 때는 1초에 1만큼 움직인다. 두 번째 방법은 점프하는 것이다. 점프를 하게 되면, T초에 D만큼 움직인다. 점프는 일직선으로만 할 수 있고, 정확하게 D칸만 움직일 수 있다.
위의 두 가지 방법을 이용해서 집에 돌아오는데 걸리는 시간의 최솟값을 구하는 프로그램을 작성하시오. 꼭 한 가지 방법만 사용해야 되는것이 아니고, 두 가지 방법을 적절히 조합해서 가장 빠른 시간을 구하는 것이다.
입력
첫째 줄에 네 정수 X, Y, D, T가 주어진다.
출력
첫째 줄에 집에 돌아오는데 걸리는 시간의 최솟값을 출력한다. 절대/상대 오차는 10^-9까지 허용한다.
문제 링크
1069번: 집으로
은진이는 지금 (X, Y)에 있고, (0, 0)에 있는 집으로 가능한 빨리 가려고 한다. 이동할 수 있는 방법은 다음 두 가지이다. 첫 번째 방법은 걷는것이다. 걸을 때는 1초에 1만큼 움직인다. 두 번째 방법
www.acmicpc.net
제한
- 1 ≤ X, Y ≤ 1,000
- 1 ≤ D, T ≤ 10,000
풀이
처음에는 점프를 하면 정확히 D'칸'만 움직일 수 있다길래, bfs나 dfs처럼 그래프의 좌표를 얘기하는 줄 알았다.
그렇게 생각하고 예제를 계속 체크해보는데 말이 안되길래 좌표축으로 소수까지 생각하고서야 문제를 이해했다.
기하를 쓰는 문제인가 싶었지만, 기하를 쓰는 건 두 점 사이의 거리에서 뿐이었다.
여러 개의 조건 분기로 모든 경우의 수를 다 체크 할 수 있으므로 조건만 잘 걸어주면 되는 문제였다.
프로그램 동작
일어날 수 있는 모든 조건을 하나씩 체크해보자.
1. 점프하는 속도보다 걸어가는 속도가 빠를 때
점프하는 이유는 걸어가는 것보다 빠르기 때문인데, 점프 속도가 1보다 낮으면 점프할 이유가 없으니 전부 걸어가는 걸로 계산한다.▼
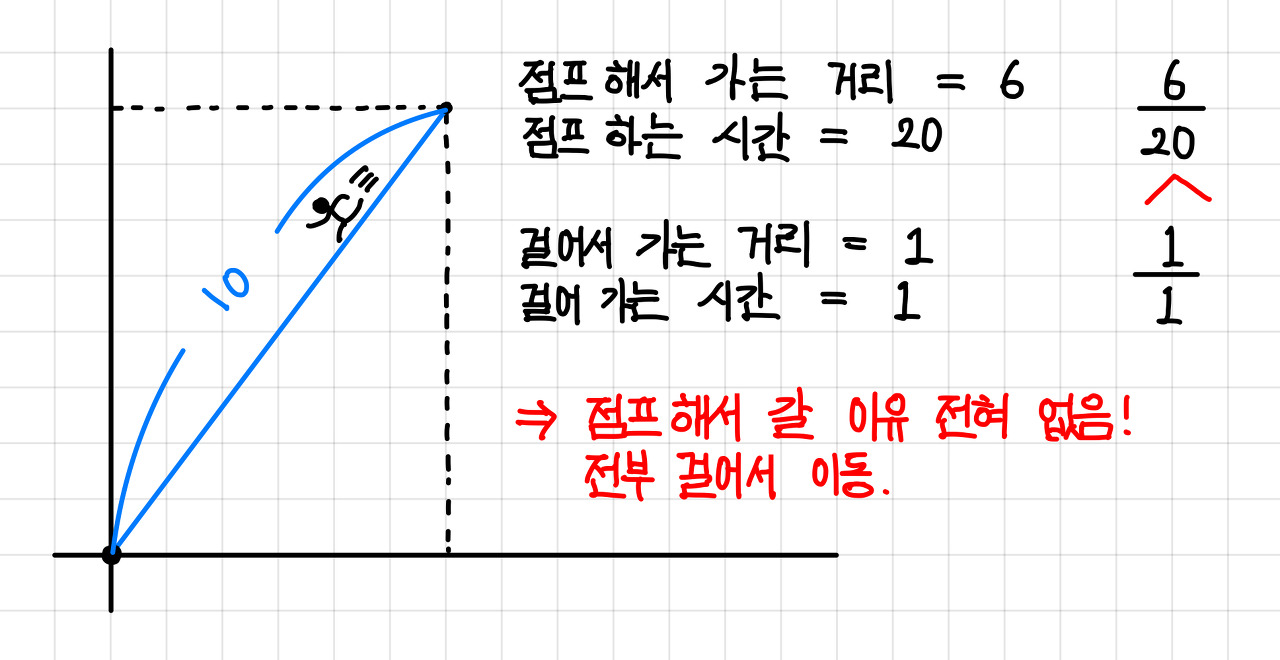
2. 점프만으로 도착지에 정확히 착지
점프만으로 도착지에 정확하게 도달할 수 있다면 점프한 횟수와 점프하는 시간을 곱해주면 답이 된다.▼
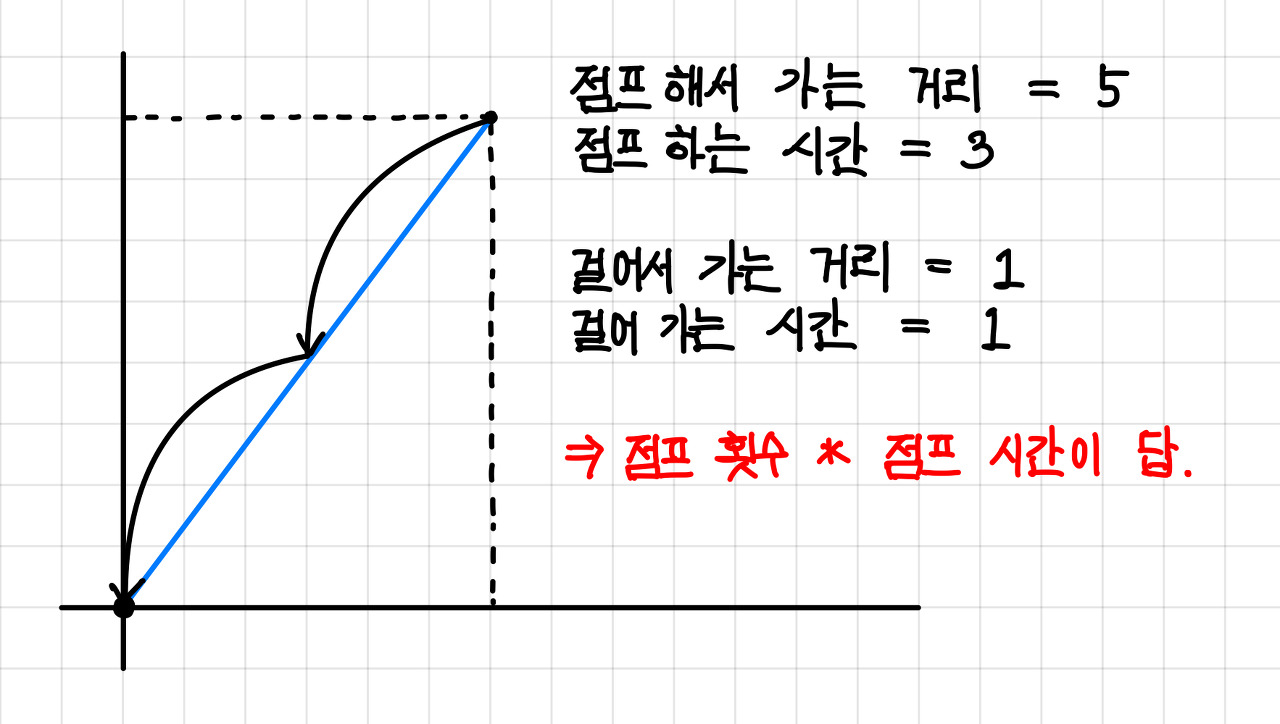
3. 점프를 했는데 도착지에 덜/더 도착
이 경우 점프를 할 수 있는 만큼(도착지를 넘지 않게) 하고, 남은 거리에 대해서 다시 생각을 해본다.▼
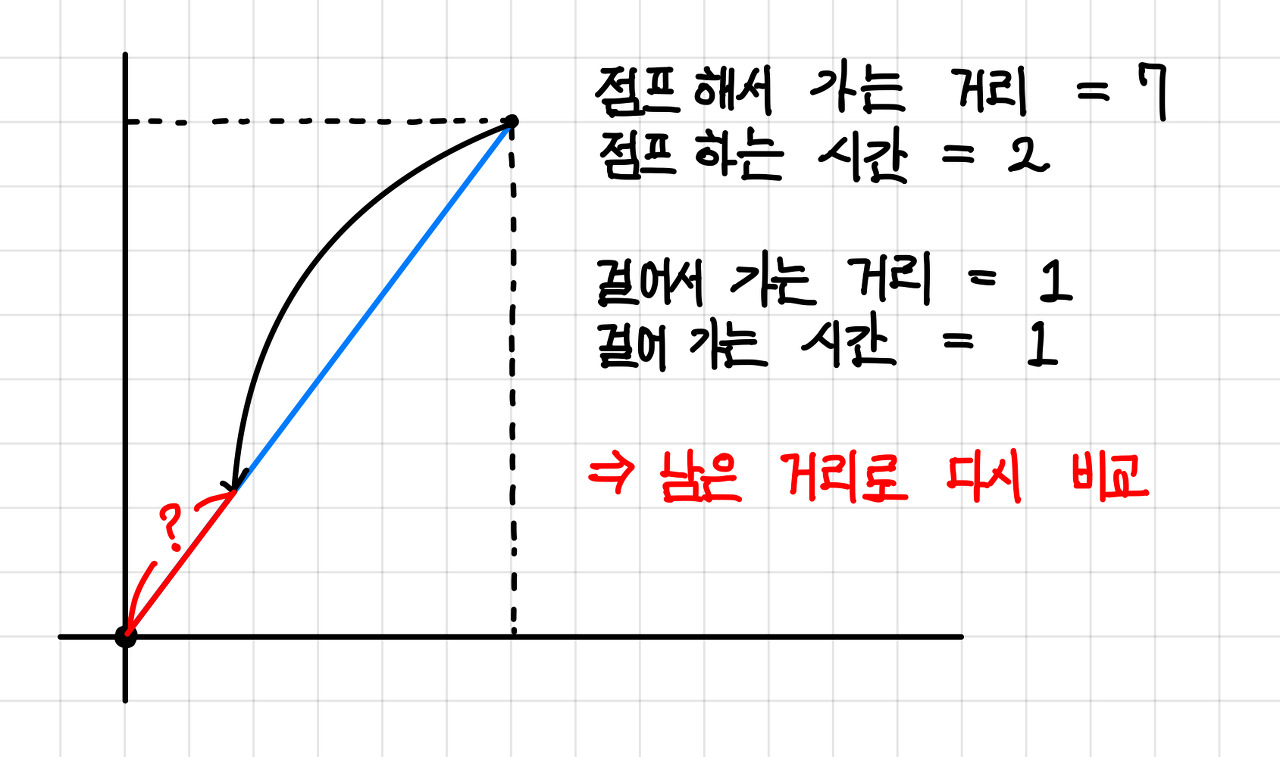
특정 거리를 점프 두번으로 꺾어 가기
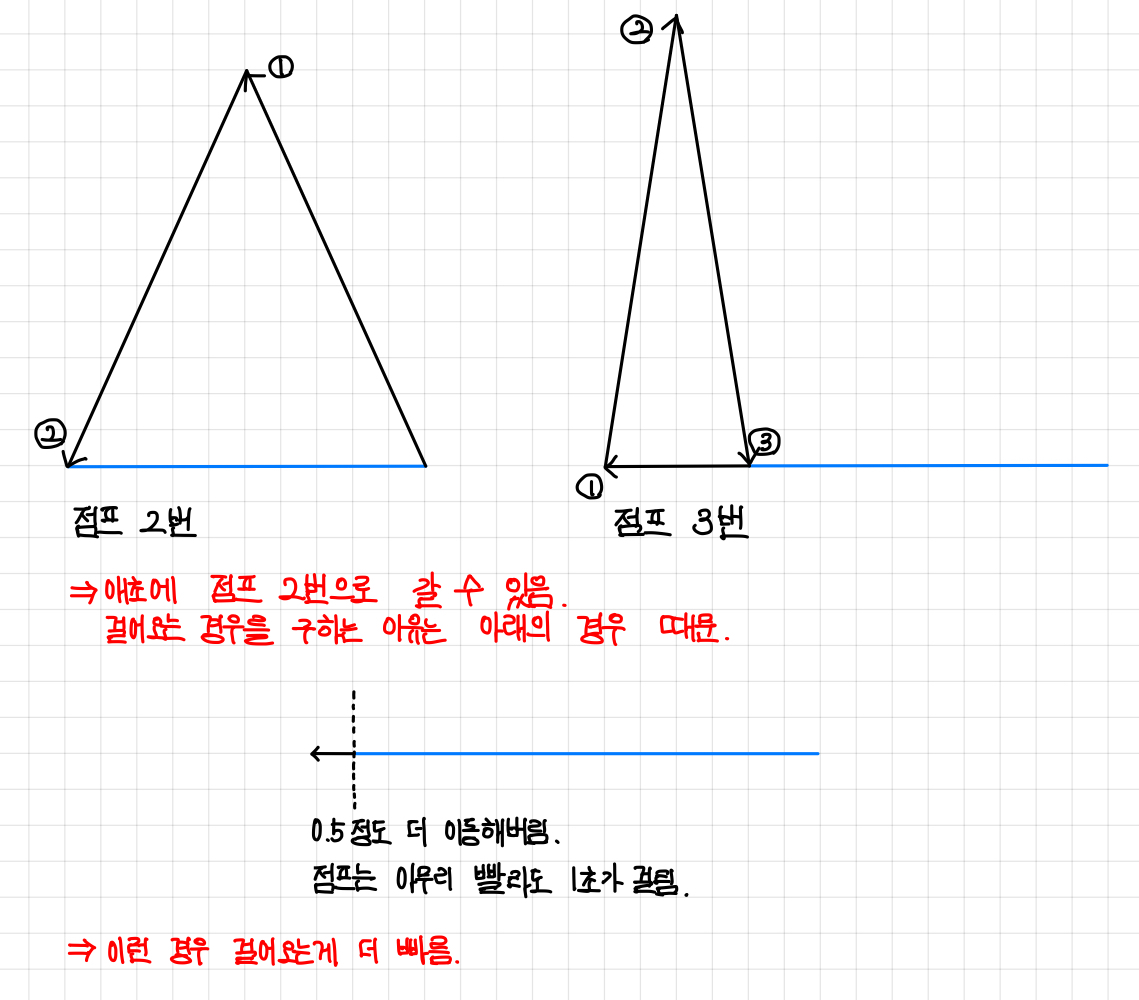
지금까지는 목적지를 향한 직선 거리를 이동하고 점프했는데, 마지막 부분에서는 꺾어서 점프하는 것도 생각할 수 있다.
아래와 같이 파란색 거리를 두 번 꺾어서, 삼각형 모양으로 이동할 수 있다.▼
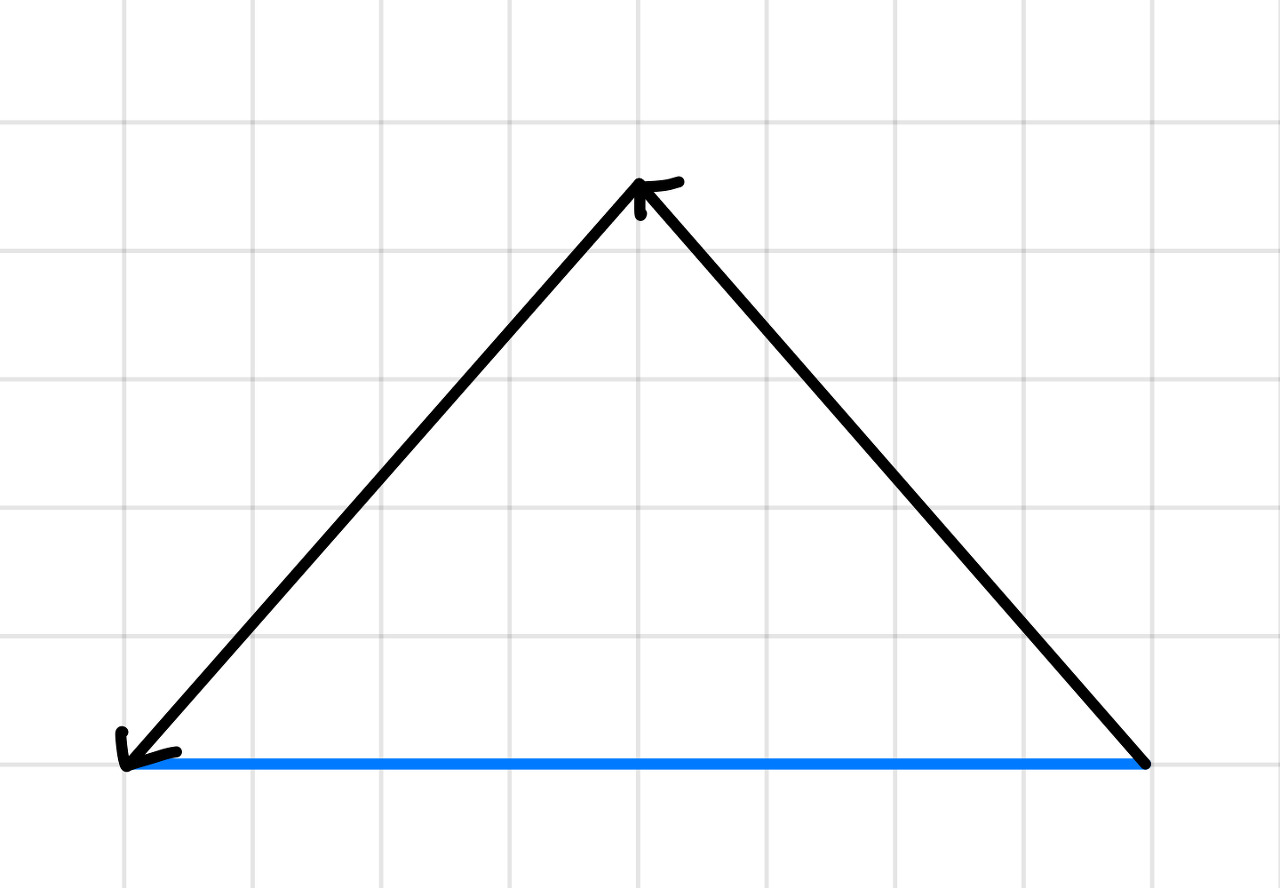
더 간 후 걸어서 돌아오기
목적지가 (0, 0)에 있다고 했지 갈 수 있는 모든 좌표가 양수라는 얘기는 하지 않았다.
따라서 초과해서 간 후 걸어서 돌아올 수 있다.
그러면 초과해서 간 후, 초과한 범위를 점프 두 번으로 꺾어 오는게 더 빠르지 않을까 생각할 수 있다.
하지만 그럴 거면 처음부터 점프 두 번으로 꺾어 갈 수 있기에 그 경우는 구할 필요가 없다.
걸어오는 경우를 구하는 이유는 정말 간발의 차이로 빗겨나가는 경우나, 점프 시간이 오래걸리는 경우 걸어오는게 더 빠를 수 있기 때문이다.▼
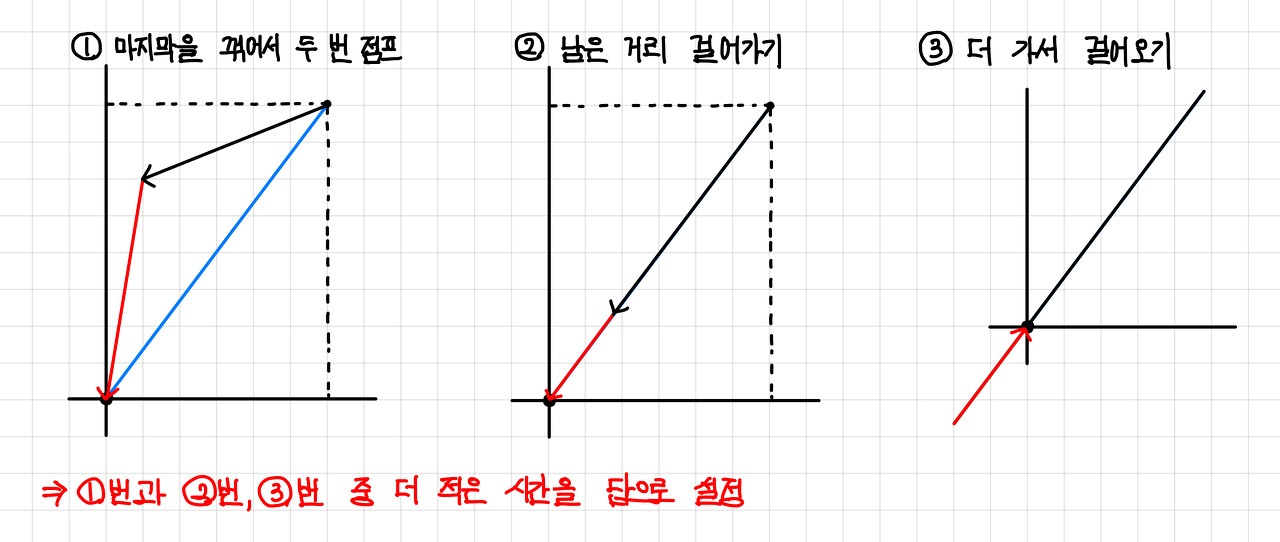
점프 했을 때의 경우들
- 1번 : 마지막에 두 번 점프
- 2번 : 남은 거리 걸어 가기
- 3번 : 더 가서 걸어 오기
이 세 경우를 구해서 더 작은 값을 답으로 설정하면 된다.▼
이렇게 경우를 설정하면 모든 경우에 대해서 구할 수 있다.
해당 경우들의 조건문만 잘 설정해서 답을 출력하면 된다.
C++ 코드
#include <iostream>
#include <cmath>
#include <algorithm>
#define MIN(x, y)(x < y ? x : y)
using namespace std;
double X, Y, D, T;
void input() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> X >> Y >> D >> T;
}
void solution() {
double dist, answer, tmp;
int cnt;
dist = sqrt(X * X + Y * Y);
answer = dist;
if (D / T < 1) {
cout.precision(13);
cout << answer << '\n';
return ;
}
cnt = dist / D;
answer = cnt * T;
dist -= cnt * D;
if (dist != 0) {
if (cnt != 0)
tmp = answer + T;
else
tmp = min(T * 2, D - dist + T);
answer += dist;
answer = min(answer, tmp);
}
cout.precision(13);
cout << answer << '\n';
}
void solve() {
input();
solution();
}
int main() {
solve();
}
'Algorithm > PS' 카테고리의 다른 글
| 백준 1865번 웜홀 - SWIFT (0) | 2024.04.02 |
|---|---|
| 백준 1780번 종이의 개수 - SWIFT (0) | 2024.03.13 |
| 백준 1753번 최단경로 - SWIFT (0) | 2024.03.10 |
| 백준 1747번 소수&팰린드롬 - SWIFT (0) | 2024.03.03 |
| 백준 1744번 수 묶기 - SWIFT (0) | 2024.03.01 |




