

문제
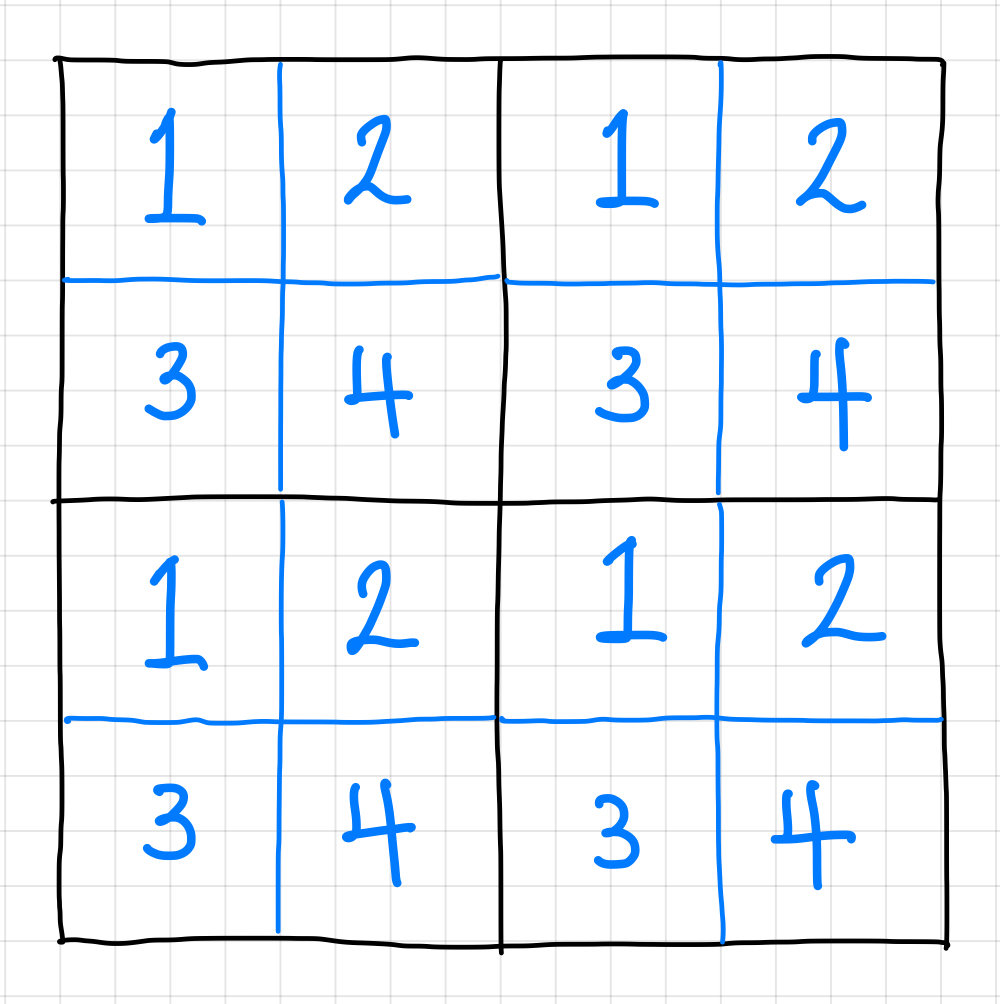
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
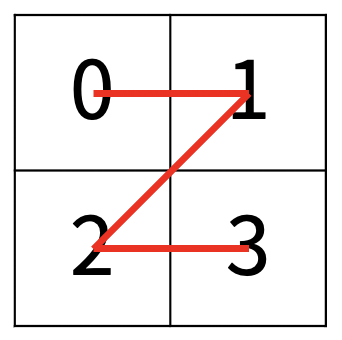
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 4 × 4 크기의 배열을 방문한 순서이다.
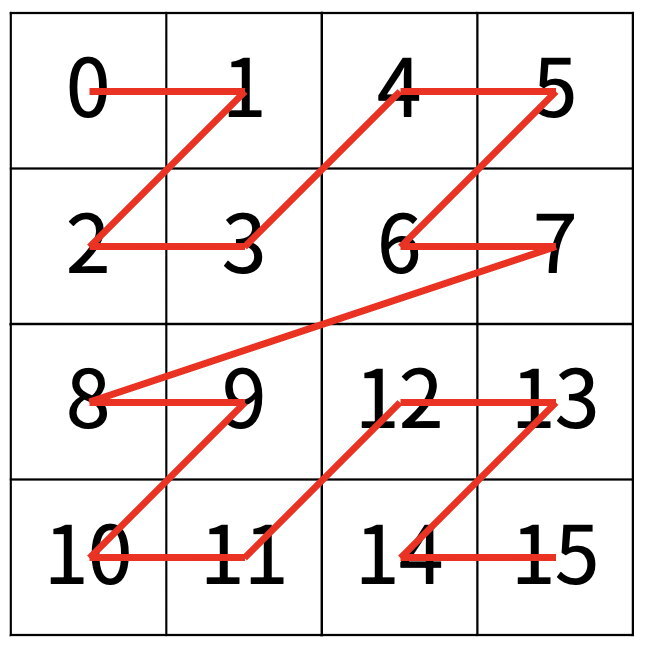
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
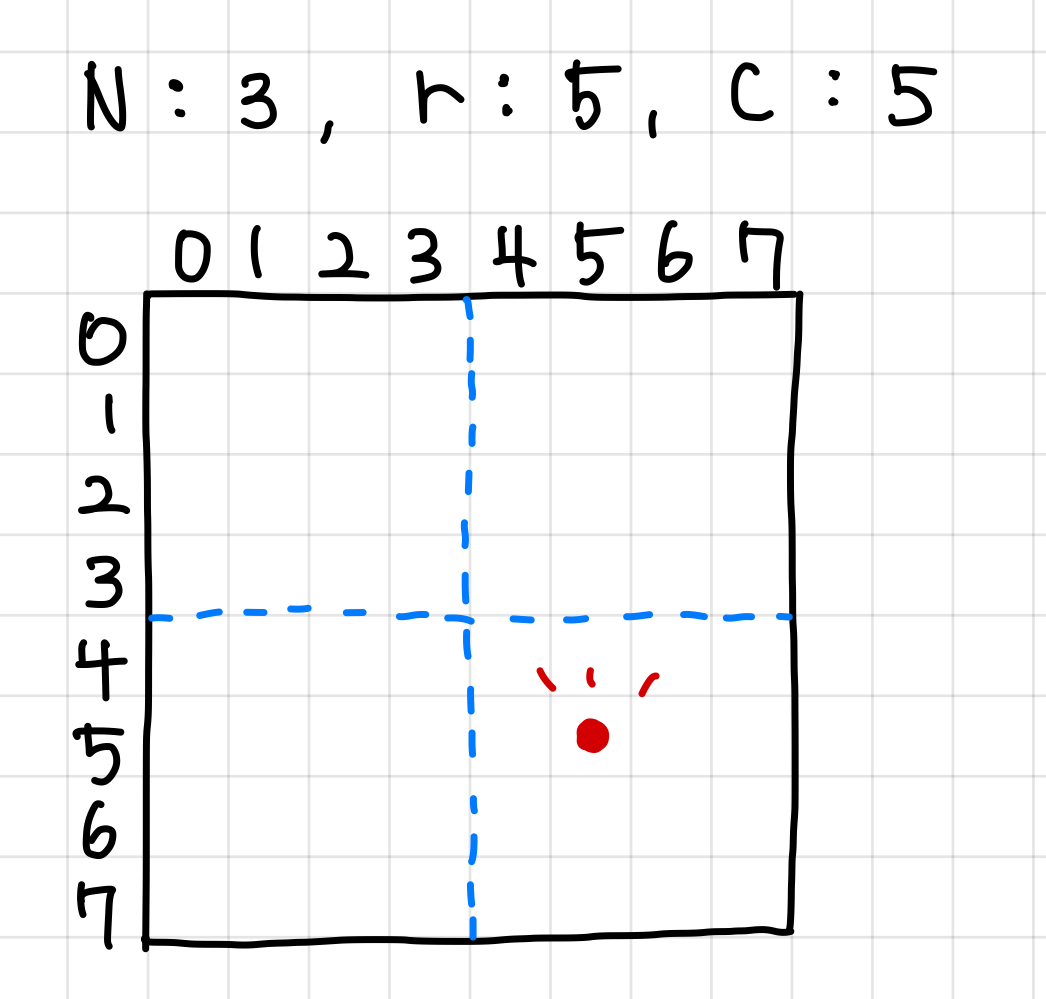
다음은 N=3일 때의 예이다.
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
문제 링크
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
풀이
재귀를 적극 사용하면 쉽게 풀 수 있는 문제다.
다른 사람의 풀이를 보니까, 무슨 한 줄로도 풀던데 아무리 봐도 어떻게 한 줄로 풀리는 지 모르겠다.
일단 문제에서는 Z모양으로 그래프를 순회한다.
사분면으로 나타내면, 2 * 2 그래프를 1사분면, 2사분면, 3사분면, 4사분면 순서로 그래프를 순회한다.
그런데 이 규칙은 2의 제곱수 크기의 그래프 모두에서 적용된다.
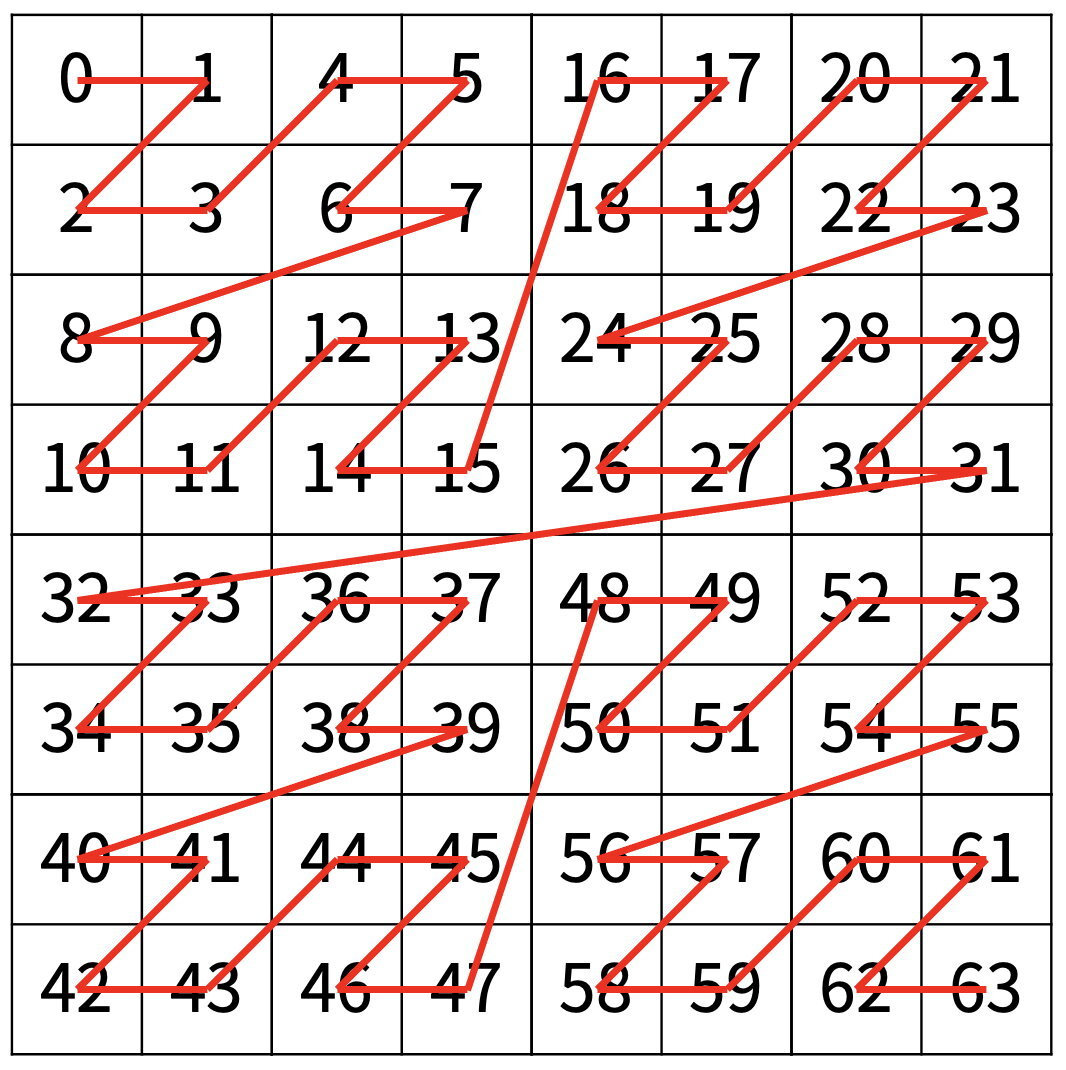
16 * 16 짜리 그래프에서는 아래 그림과 같은 순서로 순회하게 된다.▼
하지만 16 * 16 그래프의 한 사분면인 8 * 8 그래프에서도 똑같이 적용된다.▼
더 잘게 쪼개면도 가능하지만, 최대한 작게 쪼갠것이 2 * 2 크기이다.
2의 제곱수 크기라고 했으니 결국엔 2 * 2크기의 그래프 순회가 점점 더 큰 범위로 반복이 된다는 것이다.
프로그램 동작
그렇다면 그래프를 전부 순회할 거냐?
절대 아니다.
N의 범위는 1부터 15까지인데, 그래프의 크기는 2^N * 2^N이다.
만약 N이 최대 범위인 15까지 들어오면, 그래프의 원소 개수는 2^30이 된다.
Int의 양의 정수 크기가 2^31에 21억 정도 되는걸 생각하면, 1억에 대략 1초니까 10초 넘게 걸린다.
그래서 그래프를 직접 만들지 않고, 인덱스의 특성을 이용해서 풀 것이다.
1. r과 c가 그래프의 몇 사분면에 있는 지 확인한다.▼
2. 사분면에 따라 정답에 값을 더한다.▼
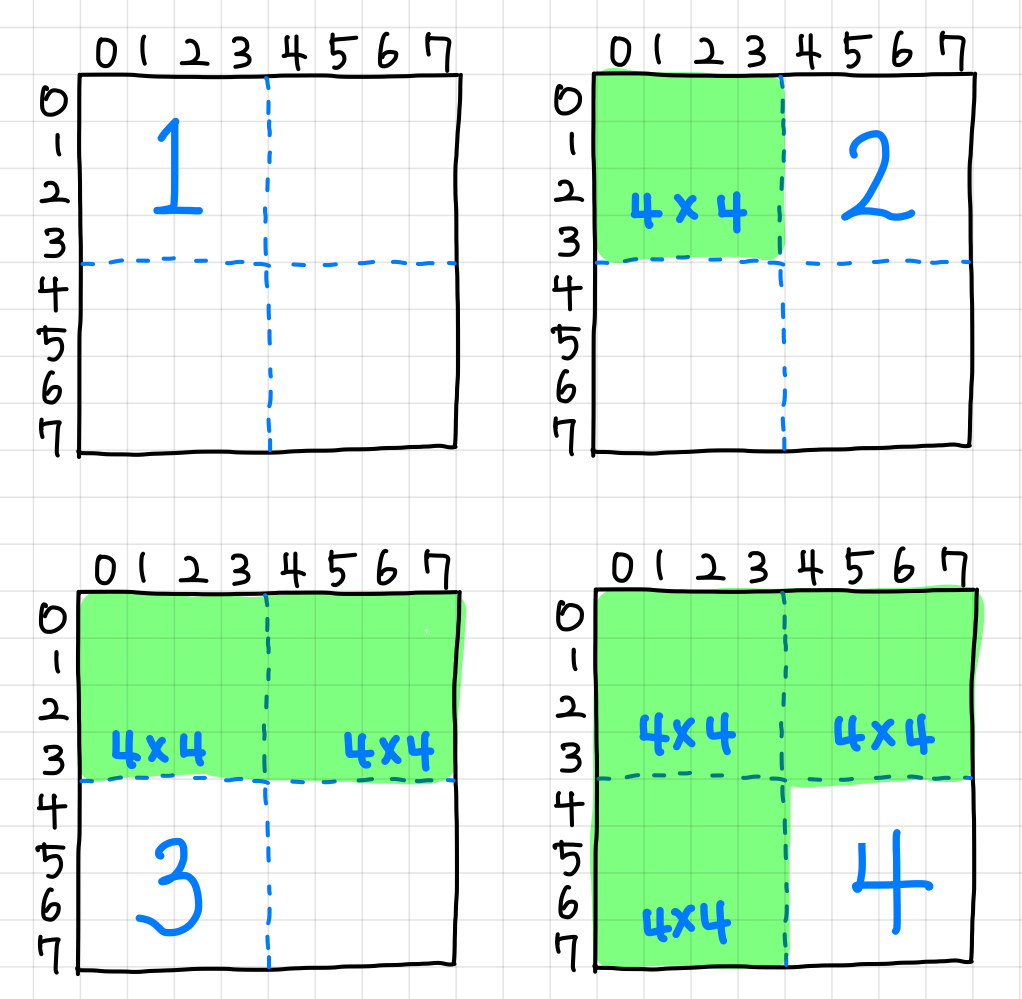
1사분면의 경우, 1사분면 이전에 순회할 사분면이 없으므로 아무 값도 더하지 않는다.
2사분면의 경우, 2사분면에 오기 전에 1사분면을 순회하므로 1사분면 크기 만큼 더해준다.
3사분면의 경우, 1, 2 사분면을 순회하므로 두 사분면의 크기 만큼 더해준다.
4사분면의 경우, 1, 2, 3 사분면을 순회하므로 세 사분면의 크기 만큼 더해준다.
현재 r, c의 경우 4사분면에 속하므로 답에 16 * 3을 더해준다.▼
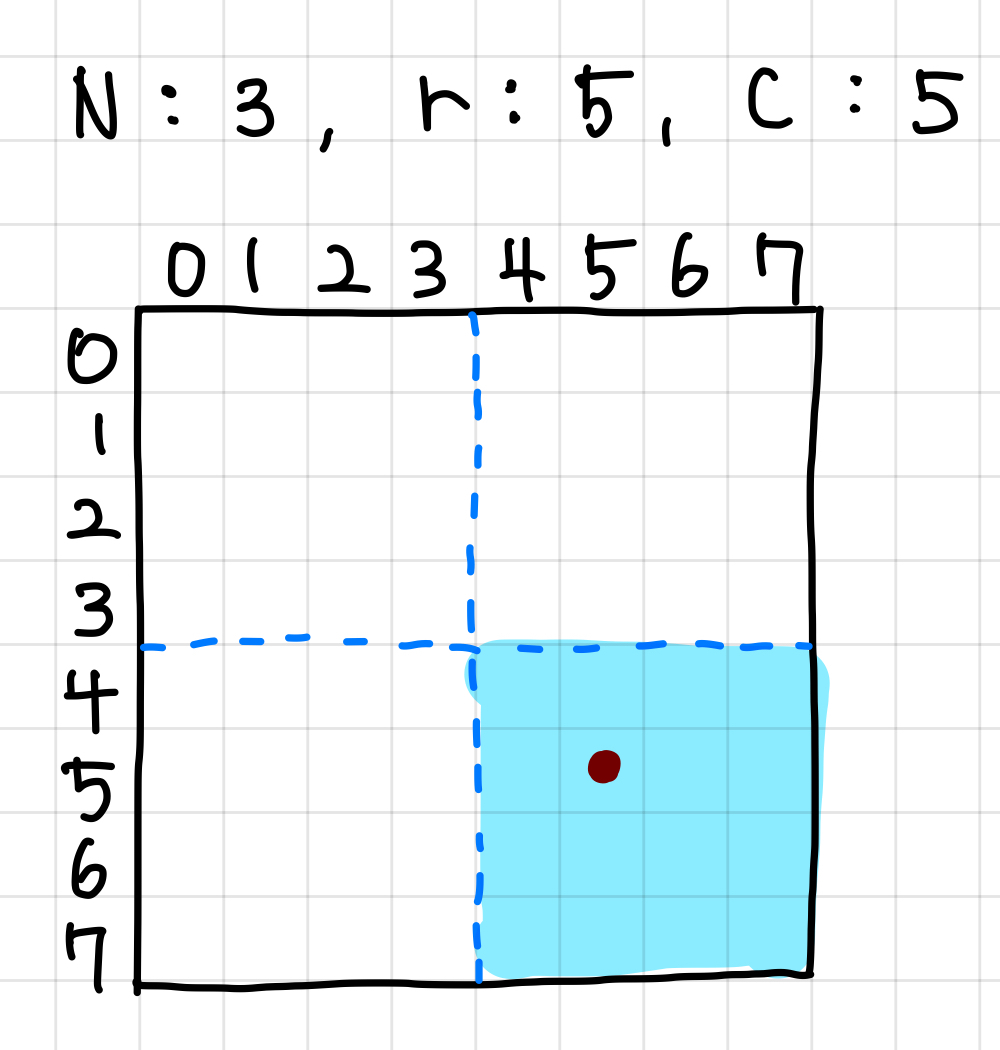
그리고 다음에는 칠해진 하늘색 영역으로 방금 했던 과정을 다시 해준다.
3. 이번에는 방금 전의 하늘색 영역에 해당하는 4 * 4 영역에서 점이 어느 사분면에 있는지 확인한다.
이 영역에서 점은 1사분면에 있으므로 아무 값도 더하지 않는다.
앞의 과정을 다시 하늘색으로 칠한 영역으로 반복해준다.▼
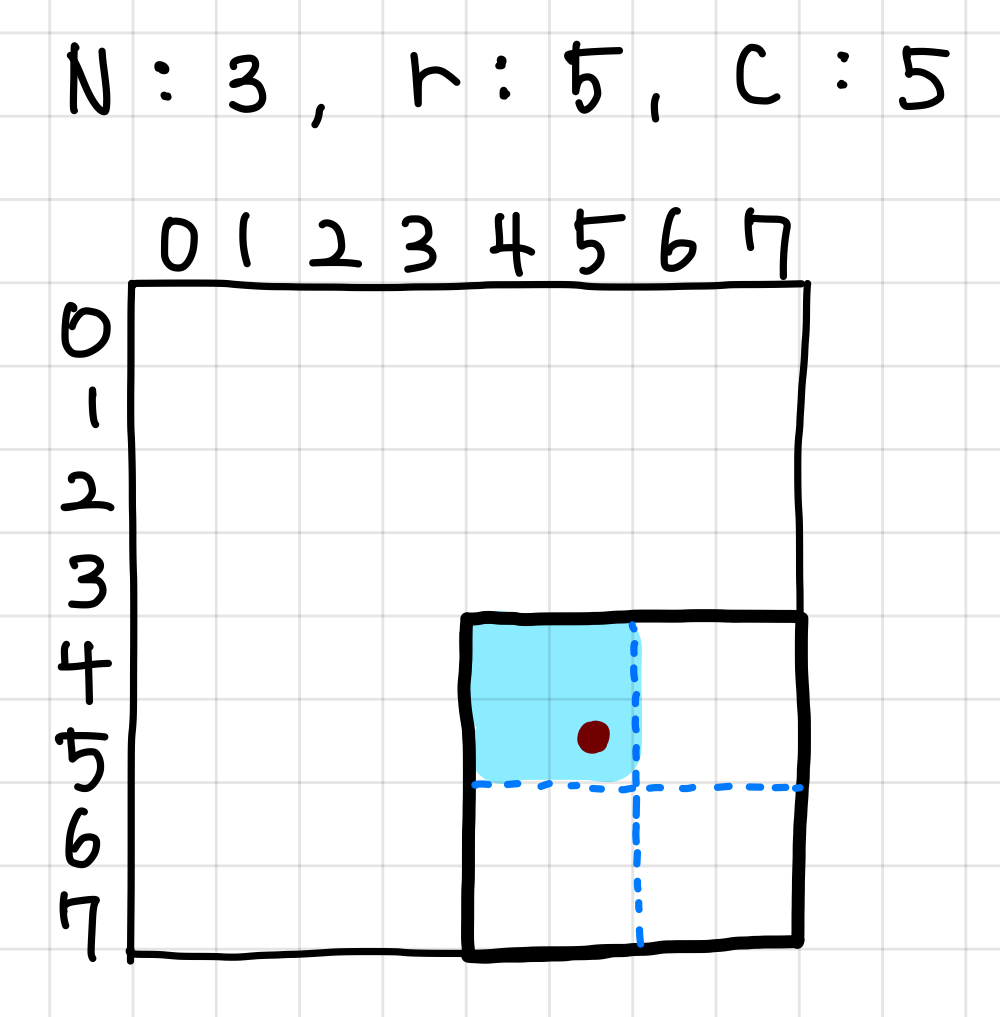
4. 3번 과정 처럼 방금 전의 하늘색 영역에 해당하는 영역에서 점이 어느 사분면에 있는 지 확인하는데, 현재 하늘색 영역은 최소 단위 이므로 값을 더해주고 함수를 끝낸다.▼
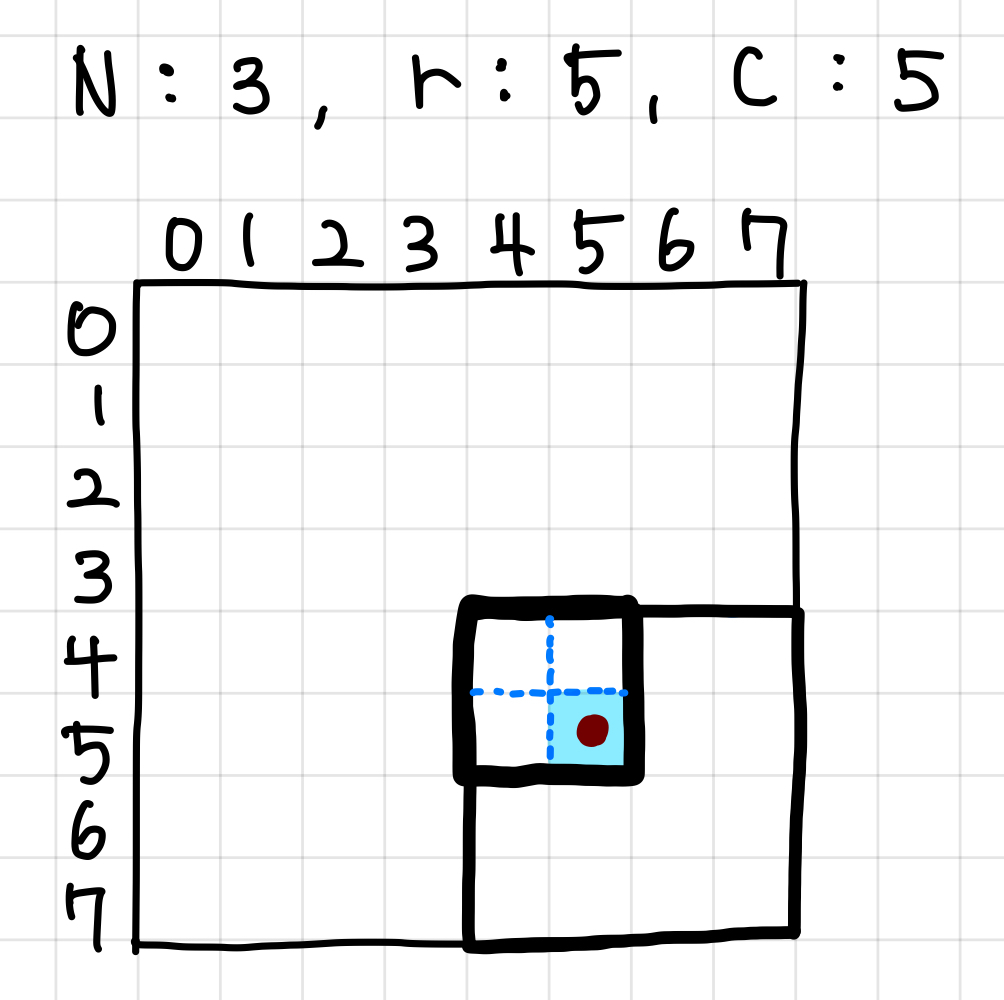
이번엔 4사분면에 있으므로 정답에 3을 더해준다.
정답은 51이 된다.
5. 정답을 출력해준다.
Swift 코드
import Foundation
let Nrc = readLine()!.split(separator: " ").map { Int(String($0))! }
let N = Nrc[0], r = Nrc[1], c = Nrc[2]
var answer = 0
func find(_ minY: Int,_ minX: Int, _ maxY: Int, _ maxX: Int) {
if (r >= minY && r <= minY + (maxY - minY - 1) / 2) && (c >= minX && c <= minX + (maxX - minX - 1) / 2) {
if maxY - minY == 2 {
return
} else {
find(minY, minX, minY + (maxY - minY) / 2, minX + (maxX - minX) / 2)
}
} else if (r >= minY && r <= minY + (maxY - minY - 1) / 2) && (c >= minX + (maxX - minX) / 2 && c <= maxX - 1) {
if maxY - minY == 2 {
answer += 1
return
} else {
answer += (maxY - minY) * (maxY - minY) / 4
find(minY, minX + (maxX - minX) / 2, minY + (maxY - minY) / 2, maxX)
}
} else if (r >= minY + (maxY - minY) / 2 && r <= maxY - 1) && (c >= minX && c <= minX + (maxX - minX - 1) / 2) {
if maxY - minY == 2 {
answer += 2
return
} else {
answer += (maxY - minY) * (maxY - minY) * 2 / 4
find(minY + (maxY - minY) / 2, minX, maxY, minX + (maxX - minX) / 2)
}
} else if (r >= minY + (maxY - minY) / 2 && r <= maxY - 1) && (c >= minX + (maxX - minX) / 2 && c <= maxX - 1) {
if maxY - minY == 2 {
answer += 3
return
} else {
answer += (maxY - minY) * (maxY - minY) * 3 / 4
find(minY + (maxY - minY) / 2, minX + (maxX - minX) / 2, maxY, maxX)
}
}
}
find(0, 0, Int(pow(Double(2), Double(N))), Int(pow(Double(2), Double(N))))
print(answer)
처음에는 그냥 구간을 2로 나누면 다음 구간이 되겠지 하고 그냥 막 나눠서 다음 인수로 넘겼는데, 그렇게 하면 min값과 max값이 같아지는 경우가 생긴다.
그래서 최솟값에 min과 max값의 차이의 절반을 더해주는 식으로 인자를 전달해야 제대로 실행된다.
좀 더 세련되게는 풀 수 있을 거 같은데, 여전히 한 줄로 정답을 내는건 이해가 안된다...
'Algorithm > PS' 카테고리의 다른 글
| 백준 1152번 단어의 개수 - SWIFT, C++ (0) | 2024.02.13 |
|---|---|
| 백준 1149번 RGB거리 - SWIFT (0) | 2024.02.13 |
| 백준 1068번 트리 - SWIFT (0) | 2024.02.08 |
| 백준 1021번 회전하는 큐 - SWIFT (0) | 2024.02.06 |
| 백준 1019번 책 페이지 - SWIFT (0) | 2024.02.06 |




